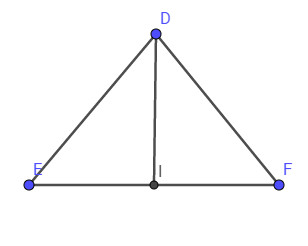
Câu 30 trang 67 SGK Hình học 10: Ôn tập Chương II - Tích vô hướng của hai vectơ và ứng dụng. Cho tam giác DEF có DE = DF =10cm và EF = 12cm. Gọi I là trung điểm của cạnh EF. Đoạn thẳng DI có độ dài là:
Bài 30. Cho tam giác \(DEF\) có \(DE = DF =10cm\) và \(EF = 12cm\). Gọi \(I\) là trung điểm của cạnh \(EF\). Đoạn thẳng \(DI\) có độ dài là:
A. \(6,5 cm\) B. \(7cm\)
C. \(8cm\) D. \(4cm\)
Advertisements (Quảng cáo)
Ta có: \(DI\) là đường trung tuyến của tam giác \(DEF\)
Áp dụng công thức tính độ dài đường trung tuyến: \({m_a}^2 = {{{b^2} + {c^2}} \over 2} - {{{a^2}} \over 4}\)
\(\eqalign{
& D{I^2} = {{{{10}^2} + {{10}^2}} \over 2} - {{{{12}^2}} \over 4} = 64 \cr
& \Rightarrow DI = \sqrt {64} = 8cm \cr} \)
Vậy chọn C.
