Bài 4. Cho đường thẳng \(Δ: x – y + 2\) và hai điểm \(O(0; 0); A(2; 0)\)
a) Tìm điểm đối xứng của \(O\) qua \(Δ\)
b) Tìm điểm \(M\) trên \(Δ\) sao cho độ dài đường gấp khúc \(OMA\) ngắn nhất.
a) Gọi \(H\) là hình chiếu của \(O\) trên \(Δ, H\) là giao điểm của đường thẳng qua \(O\) và vuông góc với \(Δ\).
\(\overline {OH} = (x;y)\)
\( Δ: x – y + 2 = 0\) có vecto chỉ phương \(\overrightarrow u (1;1)\)
\(\overrightarrow {OH} \bot \Delta \Rightarrow 1.x + 1.y = 0 \Leftrightarrow x + y = 0\)
Tọa độ điểm \(H\) là nghiệm của hệ phương trình:
\(\left\{ \matrix{
x + y = 0 \hfill \cr
x - y + 2 = 0 \hfill \cr} \right. \Rightarrow H( - 1;1)\)
Gọi \(O’\) là đỉnh đối xứng của \(O\) qua \(Δ\) thì \(H\) là trung điểm của đoạn thẳng \(OO’\)
\(\eqalign{
& {x_H} = {{{x_O} + {x_{O’}}} \over 2} \Leftarrow - 1 = {{0 + {x_{O’}}} \over 2} \Rightarrow {x_{O’}} = - 2 \cr
& {y_H} = {{{y_O} + {y_{O’}}} \over 2} \Leftarrow - 1 = {{0 + {y_{O’}}} \over 2} \Rightarrow {y_{O’}} = 2 \cr} \)
Advertisements (Quảng cáo)
Vậy \(O’(-2;2)\).
b) Nối \(O’A\) cắt \(Δ\) tại \(M\)
Ta có: \(OM = O’M\)
\(⇒ OM + MA = O’M + MA = O’A\)
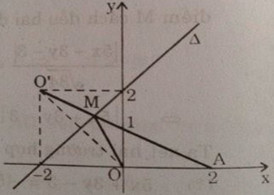
Giả sử trên \(Δ\) có một điểm \(M’ ≠ M\), ta có ngay:
\(OM’ +M’A > O’A\)
Vậy điểm \(M\), giao điểm của \(O’A\) với \(Δ\), chính là điểm thuộc \(Δ\) mà độ dài của đường gấp khúc \(OMA\) ngắn nhất.
\(A(2; 0); O(-2; 2)\) nên \(O’A\) có hệ phương trình: \(x + 2y – 2 = 0\)
Tọa độ của điểm \(M\) là nghiệm của hệ:
\(\left\{ \matrix{
x + 2y - 2 = 0 \hfill \cr
x - y + 2 = 0 \hfill \cr} \right. \Rightarrow M( - {2 \over 3},{4 \over 3})\)
