1.Lập phương trình đường tròn có tâm và bán kính cho trước
Phương trình đường tròn có tâm \(I(a; b)\), bán kính \(R\) là :
$${(x - a)^2} + {(y - b)^2} = {R^2}$$
2. Nhận xét
Phương trình đường tròn \({(x - a)^2} + {(y - b)^2} = {R^2}\) có thể được viết dưới dạng
$${x^2} + {y^2} - 2ax - 2by + c = 0$$
trong đó \(c = {a^2} + {b^2} + {R^2}\)
Ngược lại, phương trình \({x^2} + {y^2} - 2ax - 2by + c = 0\) là phương trình của đường tròn \((C)\) khi và chỉ khi \({a^2} + {b^2}-c>0\). Khi đó đường tròn \((C)\) có tâm \(I(a; b)\) và bán kính \(R = \sqrt{a^{2}+b^{2} - c}\)
Advertisements (Quảng cáo)
3.Phương trình tiếp tuyến của đường tròn
Cho điểm \({M_0}({x_0};{y_0})\) nằm trên đường tròn \((C)\) tâm \(I(a; b)\).Gọi \(∆\) là tiếp tuyến với \((C)\) tại \(M_0\)
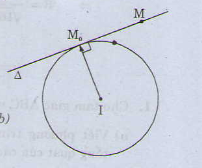
Ta có \(M_0\) thuộc \(∆\) và vectơ \(\vec{IM_{0}}=({x_0} - a;{y_0} - b)\) là vectơ pháp tuyến cuả \( ∆\)
Do đó \(∆\) có phương trình là :
$$({x_0} - a)(x - {x_0}) + ({y_0} - b)(y - {y_0}) = 0$$
Phương trình (1) là phương trình tiếp tuyến của đường tròn \({(x - a)^2} + {(y - b)^2} = {R^2}\) tại điểm \(M_0\) nằm trên đường tròn.
