
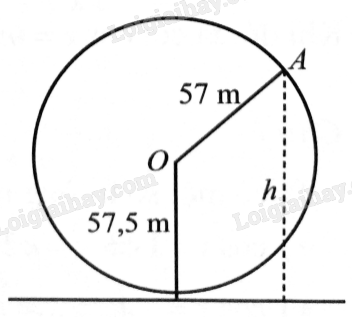
Một vòng quay trò chơi có bán kinh 57 m, trục quay cách mặt đất 57,5 m, quay đều mỗi vòng hết 15 phút. Khi vòng quay quay đều, khoảng cách \(h\) (m) từ một cabin gắn tại điểm \(A\) của vòng quay đến mặt đất được tính bởi công thức \(h\left( t \right) = 57\sin \left( {\frac{{2\pi }}{{15}}t - \frac{\pi }{2}} \right) + 57,5\); với \(t\) là thời gian quay của vòng quay tính bằng phút \(\left( {t \ge 0} \right)\) (Xem hình vẽ)
a) Tính chu kì của hàm số \(h\left( t \right)\)
b) Khi \(t = 0\) (phút) thì khoảng cách của cabin đến mặt đất bằng bao nhiêu?
c) Khi quay một vòng lần thứ nhất tính từ thời điểm \(t = 0\) (phút), tại thời điểm nào của \(t\) thì cabin ở vị trí cao nhất? Ở vị trí đạt được chiều cao 86 m?

a) Chu kì của hàm số chính là thời gian bán kính vòng quay quay hết 1 vòng.
b) Thay \(t = 0\) vào hàm số \(h\left( t \right)\) để tính khoảng cách của cabin đến mặt đất.
c) Cabin ở vị trí cao nhất khi hàm số \(h\left( t \right)\) đạt giá trị lớn nhất. Sử dụng tính chất \( - 1 \le \sin x \le 1\) để tìm giá trị lớn nhất của hàm \(h\left( t \right)\).

Advertisements (Quảng cáo)
a) Chu kì của hàm số chính là thời gian bán kính vòng quay quay hết 1 vòng. Do vòng quay trò chơi quay mỗi vòng hết 15 phút, chu kì của hàm số này là 15 phút.
b) Khoảng cách của cabin đến mặt đất tại thời điểm \(t = 0\) (phút) là:
\(h\left( 0 \right) = 57\sin \left( { - \frac{\pi }{2}} \right) + 57,5 = 0,5\) (m)
c) Do \(\sin \left( {\frac{{2\pi }}{{15}}t - \frac{\pi }{2}} \right) \le 1 \Rightarrow 57\sin \left( {\frac{{2\pi }}{{15}}t - \frac{\pi }{2}} \right) \le 57 \Rightarrow h\left( t \right) \le 114,5\)
Dấu bằng xảy ra \( \Leftrightarrow \sin \left( {\frac{{2\pi }}{{15}}t - \frac{\pi }{2}} \right) = 1 \Leftrightarrow \frac{{2\pi }}{{15}}t - \frac{\pi }{2} = \frac{\pi }{2} + k2\pi \Leftrightarrow \frac{{2\pi }}{{15}}t = \pi + k2\pi \)
\( \Leftrightarrow t = \frac{{15}}{2} + 15k\) \(\left( {k \in \mathbb{Z}} \right)\)
Như vậy, kể từ thời điểm \(t = 0\) (phút), cabin đạt vị trí cao nhất tại thời điểm \(t = 7,5\) (phút)
Để tìm thời gian cabin đạt độ cao 86 m, ta cần phải tìm các giá trị của \(t\) để \(h\left( t \right) = 86\).
Ta có \(h\left( t \right) = 86 \Rightarrow 57\sin \left( {\frac{{2\pi }}{{15}}t - \frac{\pi }{2}} \right) + 57,5 = 86 \Rightarrow \sin \left( {\frac{{2\pi }}{{15}}t - \frac{\pi }{2}} \right) = \frac{1}{2}\)
Theo Bài 46, ta có \(\sin \left( {\frac{{2\pi }}{{15}}t - \frac{\pi }{2}} \right) = \frac{1}{2} \Leftrightarrow \left[ \begin{array}{l}\frac{{2\pi }}{{15}}t - \frac{\pi }{2} = \frac{\pi }{6} + k2\pi \\\frac{{2\pi }}{{15}}t - \frac{\pi }{2} = \frac{{5\pi }}{6} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t = 5 + 15k\\t = 10 + 15k\end{array} \right.\)
Như vậy, kể từ thời điểm \(t = 0\) (phút), cabin đạt được chiều cao 86 m lần đầu tiên khi \(t = 5\) (phút)
