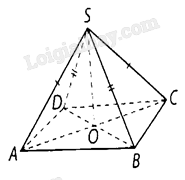
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi tâm \(O\) và \(SA = SC\), \(SB = SD\). Chứng minh rằng
a) \(SO \bot \left( {ABCD} \right)\);
b) \(AC \bot \left( {SBD} \right)\) và \(BD \bot \left( {SAC} \right)\).

a) Chứng minh tam giác \(SAC,SBD\) cân, \(O\) là trung điểm \(AC,BD\) từ đó suy ra
\(SO \bot AC,BD \Rightarrow SO \bot \left( {ABCD} \right)\).
b) Chứng minh \(AC \bot BD,AC \bot SO\) suy ra \(AC \bot \) (SBD).
Advertisements (Quảng cáo)
Chứng minh \(AC \bot BD,BD \bot SO\) suy ra \(AC \bot \) (SBD).

a) Vì \(O\) là giao điểm của \(AC\) và \(BD\) nên \(O\) là trung điểm của \(AC\) và \(BD\) suy ra tam giác \(SAC,SBD\) cân, suy ra \(SO \bot AC,SO \bot BD\).
Do đó \(SO \bot \left( {ABCD} \right)\).
b) Vì \(AC \bot BD,AC \bot SO\) nên \(AC \bot \) (SBD).
Tương tự, ta được \(BD \bot \left( {SAC} \right)\).