
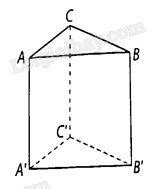
Cho hình lăng trụ tam giác \(ABC \cdot A’B’C’\) có \(AA’\) vuông góc với mặt phẳng \(\left( {ABC} \right)\) và đáy là tam giác \(ABC\) vuông tại \(B\). Chứng minh rằng:
a) \(B’B \bot \left( {A’B’C’} \right)\);
b) \(B’C \bot \left( {ABB’A’} \right)\)

Advertisements (Quảng cáo)
a) Áp dụng tính chất hai mặt đáy của hình lăng trụ song song với nhau
Chỉ ra \(AA’ \bot \left( {ABC} \right),AA’//BB’,\left( {ABC} \right)//\left( {A’B’C’} \right)\);
b) Chỉ ra \(BC \bot AB,BC \bot BB’\) và \(BC//B’C’ \Rightarrow B’C’ \bot \left( {ABB’A’} \right)\)

a) Vì \(AA’ \bot \left( {ABC} \right),AA’//BB’,\left( {ABC} \right)//\left( {A’B’C’} \right) \Rightarrow BB’ \bot \left( {A’B’C’} \right)\);
b) Vì \(BC \bot AB,BC \bot BB’ \Rightarrow BC \bot \left( {ABB’A’} \right)\) mà \(BC//B’C’ \Rightarrow B’C’ \bot \left( {ABB’A’} \right)\)
