
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\), tam giác \(ABC\) nhọn. Gọi \(H,K\) lần lượt là trực tâm của tam giác \(ABC\) và \(SBC\). Chứng minh rằng:
a) \(BC \bot \left( {SAH} \right)\) và các đường thẳng \(AH,BC,SK\) đồng quy;
b) \(SB \bot \left( {CHK} \right)\) và \(HK \bot \left( {SBC} \right)\).

a) Chỉ ra \(BC \bot SA,BC \bot AH\) nên \(BC \bot \left( {SAH} \right)\).
Gọi \(M\) là giao điểm của \(AH\) và \(BC\)
Chứng minh \(BC \bot AH,BC \bot SM\) suy ra \(S,K,M\) thẳng hàng
Do đó, \(SK,AH,BC\) đồng quy tại \(M\).
b) Chỉ ra \(CH \bot SB\), \(SB \bot CK\) rồi suy ra \(SB \bot \left( {CHK} \right)\).
Từ đó ta có \(SB \bot HK\), tương tự, ta chứng minh được \(SC \bot \left( {BHK} \right)\), suy ra \(SC \bot HK\). Do đó \(HK \bot \left( {SBC} \right)\).
Advertisements (Quảng cáo)

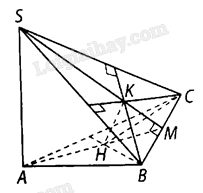
a) Chỉ ra \(BC \bot SA,BC \bot AH\) nên \(BC \bot \left( {SAH} \right)\).
Gọi \(M\) là giao điểm của \(AH\) và \(BC\)\(CH \bot AB\)
Ta có: \(BC \bot \left( {SAM} \right)\), suy ra \(BC \bot SM\), mà \(K\) là trực tâm của tam giác \(SBC\) nên \(SM\) đi qua \(K\).
Do đó, \(SK,AH,BC\) đồng quy tại \(M\).
b)
Vì \(SA \bot \left( {ABC} \right)\) nên \(SA \bot CH\), mà , suy ra \(CH \bot \left( {SAB} \right)\).
Do đó \(CH \bot SB\), lại có \(SB \bot CK\) nên \(SB \bot \left( {CHK} \right)\).
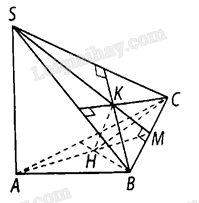
Từ đó ta có \(SB \bot HK\), tương tự, ta chứng minh được \(SC \bot \left( {BHK} \right)\), suy ra \(SC \bot HK\). Do đó \(HK \bot \left( {SBC} \right)\).
