
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông tâm \(O\) và các cạnh đều bằng \({\rm{a}}\).
a) Chứng minh rằng \(SO \bot \left( {ABCD} \right)\).
b) Tính góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {SBD} \right)\).
c) Gọi \(M\) là trung điểm của cạnh \(SC\) và \(\alpha \) là góc giữa đường thẳng \(OM\) và mặt phẳng\(\left( {SBC} \right)\). Tính \({\rm{sin}}\alpha \).

a) Chứng minh \(SO\) vuông góc với hai đường thẳng cắt nhau nằm trên \(ABCD\) rồi suy ra \(SO \bot \left( {ABCD} \right)\).
b) Chứng minh \(AO \bot \left( {SBD} \right)\)
Tìm hình chiếu vuông góc của \(SA\) trên mặt phẳng \(\left( {SBD} \right)\), do đó góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {SBD} \right)\) bằng góc giữa hai đường thẳng \(SA\) và hình chiếu của nó
c) Kẻ \(OK \bot BC\) tại \(K,OH \bot SK\) tại \(H\) thì ta chứng minh \(OH \bot \left( {SBC} \right)\),
Tìm hình chiếu vuông góc của \(OM\) trên mặt phẳng \(\left( {SBC} \right)\),
Góc giữa đường thẳng \(OM\) và mặt phẳng \(\left( {SBC} \right)\) bằng góc giữa hai đường thẳng \(OM\) và hình chiếu của nó
Advertisements (Quảng cáo)
Áp dụng tỉ số lượng giác cho tam giác vuông để tính góc

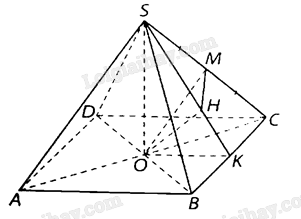
a) Ta có: \(SO \bot AC\); \(SO \bot BD\) nên \(SO \bot \left( {ABCD} \right)\).
b) Vì \(AO \bot \left( {SBD} \right)\) nên \(SO\) là hình chiếu vuông góc của \(SA\) trên mặt phẳng \(\left( {SBD} \right)\), do đó góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {SBD} \right)\) bằng góc giữa hai đường thẳng \(SA\) và \(SO\). Mà \(\left( {SA,SO} \right) = \widehat {ASO}\) nên góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {SBD} \right)\) bằng góc \(\widehat {ASO}\). Xét tam giác \(SAC\) có
\(S{A^2} + S{C^2} = A{C^2}\) và \(SA = SC\) nên tam giác \(SAC\) vuông cân tại \(S\), suy ra \(\widehat {ASO} = {45^ \circ }\). Vậy góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {SBD} \right)\) bằng \({45^ \circ }\).
c) Kẻ \(OK \bot BC\) tại \(K,OH \bot SK\) tại \(H\) thì ta chứng minh được \(OH \bot \left( {SBC} \right)\),
suy ra HM là hình chiếu vuông góc của \(OM\) trên mặt phẳng \(\left( {SBC} \right)\),
do đó góc giữa đường thẳng \(OM\) và mặt phẳng \(\left( {SBC} \right)\) bằng góc giữa hai đường thẳng \(OM\) và \(MH\),
mà \(\left( {OM,MH} \right) = \widehat {OMH}\) nên góc giữa đường thẳng \(OM\) và mặt phẳng (SBC) bằng góc \({\rm{OMH}}\) hay \(\widehat {{\rm{OMH}}}\). Ta có: \(OM = \frac{a}{2},OK = \frac{a}{2},SO = \frac{{a\sqrt 2 }}{2}\).
Tam giác SOK vuông tại \(O\), đường cao \({\rm{OH}}\) nên \({\rm{OH}} = \frac{{{\rm{SO}} \cdot {\rm{OK}}}}{{SK}} = \frac{{a\sqrt 6 }}{6}\).
Vì tam giác \(OMH\) vuông tại \(H\) nên \({\rm{sin}}\alpha = {\rm{sin}}\widehat {OMH} = \frac{{OH}}{{OM}} = \frac{{\sqrt 6 }}{3}\).
