
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh a, biết \(\left( {SAB} \right) \bot \left( {ABCD} \right)\), \(\left( {SAD} \right) \bot \left( {ABCD} \right)\) và \(SA = a\). Tính côsin của số đo góc nhị diện \(\left[ {S,BD,C} \right]\) và góc nhị diện \(\left[ {B,SC,D} \right]\).

Để tính góc giữa hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) ta có thể thực hiện cách sau:
Tìm hai đường thẳng \(a,b\) lần lượt vuông góc với hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\).
Khi đó góc giữa hai đường thẳng \(a,b\) chính là góc giữa hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\).
\(\left\{ \begin{array}{l}a \bot \left( \alpha \right)\\b \bot \left( \beta \right)\end{array} \right. \Rightarrow \widehat {\left( {\left( \alpha \right),\left( \beta \right)} \right)} = \widehat {\left( {a,b} \right)}\).
Áp dụng tính chất: Hình vuông có hai đường chéo vuông góc
Dựa vào tỉ số lượng giác trong tam giác vuông để tìm góc
Advertisements (Quảng cáo)
Áp dụng định lý côsin trong tam giác

Ta có \(SO \bot BD,CO \bot BD\) nên góc nhị diện \(\left[ {S,BD,C} \right]\) bằng \(\widehat {SOC}\).
Vì tam giác \(SAO\) vuông tại \(A\) nên \(SO = \sqrt {S{A^2} + A{O^2}} = \frac{{a\sqrt 6 }}{2}\) và \({\rm{cos}}\widehat {SOC} = - {\rm{cos}}\widehat {SOA} = - \frac{{OA}}{{SO}} = - \frac{{\sqrt 3 }}{3}\).
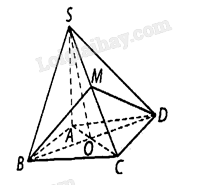
Kẻ \(BM \bot SC\) tại \(M\) thì \(DM \bot SC\) nên \(\left[ {B,SC,D} \right] = \widehat {BMD}\).
Ta có \(BC \bot \left( {SAB} \right)\) nên tam giác \(SBC\) vuông tại \(B\), tính được \(SB = a\sqrt 2 \), \(SC = a\sqrt 3 \) và \(DM = BM = \frac{{SB \cdot BC}}{{SC}} = \frac{{a\sqrt 6 }}{3}\).
Áp dụng định lý côsin trong tam giác \(BDM\), ta có: \({\rm{cos}}\widehat {BMD} = \frac{{B{M^2} + D{M^2} - B{D^2}}}{{2 \cdot BM \cdot DM}} = - \frac{3}{4}\).
