
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(A\), góc \(ABC\) bằng \({60^ \circ }\), biết tam giác \(SBC\) đều cạnh a và nằm trong mặt phẳng vuông góc với mặt phẳng \(\left( {ABC} \right)\). Tính theo a khoảng cách:
a) Từ điểm \(S\) đến mặt phẳng \(\left( {ABC} \right)\).
b) Từ điểm \(B\) đến mặt phẳng \(\left( {SAC} \right)\).
c) Giữa hai đường thẳng \(AB\) và \(SC\).

a) Tính khoảng cách từ điểm \(S\) đến mặt phẳng \(\left( {ABC} \right)\).
Bước 1: Kẻ \(SH\) vuông góc với \(BC\) tại \(H\)
Do \(\left( {SBC} \right) \bot \left( {ABC} \right) \Rightarrow SH \bot \left( {ABC} \right)\)
\( \Rightarrow d\left( {S,\left( {ABC} \right)} \right) = SH\)
Bước 2: Tính \(SH\)
b) Tính khoảng cách từ điểm \(B\) đến mặt phẳng \(\left( {SAC} \right)\).
Bước 1: Tính khoảng cách từ \(H\) đến mặt phẳng \(\left( {SAC} \right)\).
Bước 2: Nhận xét \(H\) là trung điểm của \(BC\) nên \(d\left( {B,\left( {SAC} \right)} \right) = 2d\left( {H,\left( {SAC} \right)} \right)\)c) Tính khoảng cách giữa hai đường thẳng \(AB\) và \(SC\).
Bước 1: Dựng hình bình hành \(ABMC\), chứng minh được \(ABMC\) là hình chữ nhật.
Advertisements (Quảng cáo)
Khi đó \(AB//\left( {SCM} \right)\) và mặt phẳng \(\left( {SMC} \right)\) chứa \(SC\) nên
\(d\left( {AB,SC} \right) = d\left( {AB,\left( {SCM} \right)} \right) = d\left( {B,\left( {SCM} \right)} \right) = 2d\left( {H,\left( {SCM} \right)} \right){\rm{.\;}}\)
Bước 2: Tính \(\left( {H,\left( {SCM} \right)} \right) \Rightarrow \)\(d\left( {AB,SC} \right) = d\left( {AB,\left( {SCM} \right)} \right) = 2d\left( {H,\left( {SCM} \right)} \right){\rm{.\;}}\)

a) Kẻ \(SH\) vuông góc với \(BC\) tại \(H\) thì \(SH \bot \left( {ABC} \right)\), suy ra \(d\left( {S,\left( {ABC} \right)} \right) = SH = \frac{{a\sqrt 3 }}{2}\)
b) Kẻ HK vuông góc với \(AC\) tại \(K,HQ\) vuông góc với \(SK\) tại \(Q\) thì \(d\left( {H,\left( {SAC} \right)} \right) = HQ\).
Ta có: \(AB = \frac{a}{2},HK = \frac{a}{4}\) và tam giác \(SHK\) vuông tại \(H\), đường cao \(HQ\) nên \(HQ = \frac{{SH \cdot HK}}{{SK}} = \frac{{a\sqrt {39} }}{{26}}\).
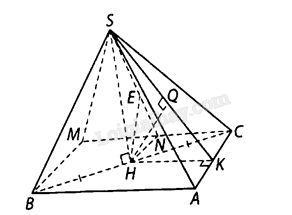
Lại có \(H\) là trung điểm của \(BC\) nên \(d\left( {B,\left( {SAC} \right)} \right) = 2d\left( {H,\left( {SAC} \right)} \right) = \frac{{a\sqrt {39} }}{{13}}\).
c) Dựng hình bình hành \(ABMC\), chứng minh được \(ABMC\) là hình chữ nhật.
Khi đó \(AB//\left( {SCM} \right)\) và mặt phẳng \(\left( {SMC} \right)\) chứa \(SC\) nên
\(d\left( {AB,SC} \right) = d\left( {AB,\left( {SCM} \right)} \right) = d\left( {B,\left( {SCM} \right)} \right) = 2d\left( {H,\left( {SCM} \right)} \right){\rm{.\;}}\)
Kẻ \(HN\) vuông góc với \(CM\) tại \(N,HE\) vuông góc với \(SN\) tại \(N\) thì \(HE \bot \left( {SCM} \right)\), suy ra \(d\left( {H,\left( {SCM} \right)} \right) = HE\).
Ta có: \(HN = \frac{{BM}}{2} = \frac{{a\sqrt 3 }}{4}\), tam giác SHN vuông tại \(H\), đường cao \(HE\) nên \(HE = \frac{{SH \cdot HN}}{{SN}} = \frac{{a\sqrt {15} }}{{10}}\).
Vậy \(d\left( {AB,SC} \right) = \frac{{a\sqrt {15} }}{5}\).
