
Người ta cắt bỏ bốn hình vuông cùng kích thước ở bốn góc của một tấm tôn hình vuông có cạnh \(1{\rm{\;m}}\) để gò lại thành một chiếc thùng có dạng hình hộp chữ nhật không nắp. Hỏi cạnh của các hình vuông cần bỏ đi có độ dài bằng bao nhiêu để thùng hình hộp nhận được có thể tích lớn nhất?

Áp dụng công thức tính thể tích khối hộp chữ nhật: \({\rm{V}} = a.b.c\).
Trong đó: \(a,b,c\) là độ dài 3 cạnh hình hộp chữ nhật có chung 1 đỉnh
Bước 1: Gọi \(x\left( {{\rm{\;m}}} \right)\) là chiều dài cạnh hình vuông nhỏ tại mỗi góc của tấm tôn được cắt bỏ đi (với \(0
Tính thể tích hình hộp chữ nhật nhận được
Bước 2: Tìm giá trị lớn nhất của thể tích hình hộp chữ nhật nhận được
Advertisements (Quảng cáo)
Từ đó tìm \(x\)

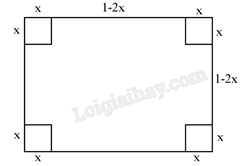
Gọi \(x\left( {{\rm{\;m}}} \right)\) là chiều dài cạnh hình vuông nhỏ tại mỗi góc của tấm tôn được cắt bỏ đi (với \(0
Thể tích hình hộp chữ nhật nhận được là
\(V = {(1 - 2x)^2} \cdot x = \frac{1}{4} \cdot \left( {1 - 2x} \right) \cdot \left( {1 - 2x} \right) \cdot 4x \le \frac{1}{4} \cdot {\left( {\frac{{1 - 2x + 1 - 2x + 4x}}{3}} \right)^3} = \frac{2}{{27}}\)
Dấu "=” xảy ra khi \(1 - 2x = 4x \Leftrightarrow x = \frac{1}{6}\).
Vậy để thể tích chiếc thùng là lớn nhất thì các cạnh của hình vuông được cắt bỏ đi là \(\frac{1}{6}{\rm{\;m}}\).
