
Cho tứ diện \(OABC\) có ba cạnh \(OA,OB,OC\) đôi một vuông góc với nhau. Gọi \(H\) là chân đường vuông góc hạ từ \(O\) đến mặt phẳng\(\left( {ABC} \right)\). Chứng minh rằng:
a)\(BC \bot \left( {OAH} \right)\);
b) \(H\) là trực tâm của tam giác \(ABC\);
c) \(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\).

- Áp dụng định lý sau
Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau thuộc cùng
một mặt phẳng thì nó vuông góc với mặt phẳng đó.
- Chứng minh hai đường thẳng vuông góc dựa vào đường thẳng vuông góc với mặt phẳng
+ \(\left\{ \begin{array}{l}a \bot \left( \alpha \right)\\b \subset \alpha \end{array} \right. \Rightarrow a \bot b\)
- Áp dụng hệ thức lượng trong tam giác vuông
a) Chứng minh \(OA \bot BC\), \(OH \bot BC\).
b) Chứng minh \(BC \bot AH\), \(CA \bot BH\) suy ra \(H\) là trực tâm của tam giác \(ABC\).
c) + Gọi \(K\) là giao điểm của \(AH\) và \(BC\),
Advertisements (Quảng cáo)
+ Chứng minh \(OK\) là đường cao của tam giác vuông \(OBC\) và \(OH\) là đường cao của tam giác vuông \(OAK\).
+ Áp dụng hệ thức lượng trong các tam giác vuông \(OBC\) và \(OAK\)

a) Vì \(OA \bot OB,OA \bot OC \Rightarrow OA \bot \left( {OBC} \right)\), suy ra. \(OA \bot BC\)
Vì \(OH \bot \left( {ABC} \right)\) nên\(OH \bot BC\),suy ra\(BC \bot \left( {OAH} \right)\).
b) Vì \(BC \bot \left( {OAH} \right)\) nên \(BC \bot AH\).
Tương tự, \(CA \bot BH\), do đó \(H\) là trực tâm của tam giác\(ABC\).
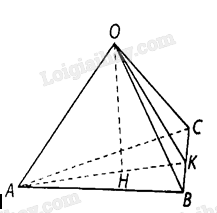
c) Gọi \(K\) là giao điểm của \(AH\) và \(BC\),
Ta có: \(OK \bot BC\) và \(OA \bot OK\) nên \(OK\) là đường cao của tam giác vuông \(OBC\) và là đường cao của tam giác vuông \(OAK\).
Áp dụng hệ thức lượng trong các tam giác vuông \(OBC\) và\(OAK\), ta có: \(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{K^2}}}\) và \(\frac{1}{{O{K^2}}} = \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\).
Từ đó suy ra: \(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\).
