Gọi \(M\) là trung điểm của \(BC\) chứng minh \(BC \bot \left( {AMD} \right)\), suy ra \(BC \bot AD\). Hướng dẫn trả lời - Bài 7.8 trang 28 sách bài tập toán 11 - Kết nối tri thức với cuộc sống - Bài 23. Đường thẳng vuông góc với mặt phẳng. Cho tứ diện \(ABCD\) có \(AB = AC\) và \(DB = DC\). Chứng minh rằng \(AD \bot BC\)...

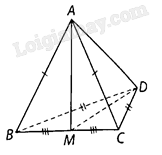
Cho tứ diện \(ABCD\) có \(AB = AC\) và \(DB = DC\). Chứng minh rằng \(AD \bot BC\).

Gọi \(M\) là trung điểm của \(BC\) chứng minh \(BC \bot \left( {AMD} \right)\), suy ra \(BC \bot AD\).
Advertisements (Quảng cáo)

Gọi \(M\) là trung điểm của \(BC\), ta có: \(BC \bot AM,BC \bot MD\).
Do đó \(BC \bot \left( {AMD} \right)\), suy ra \(BC \bot AD\).