Câu 16 trang 117 Sách bài tập Hình học 11 Nâng cao. Cho hình chóp S.ABCD có đáy là hình thoi, cạnh bên SA = AB và SA vuông góc với BC.. Bài 2 3 4: Hai đường thẳng vuông góc. Đường thẳng vuông góc với mặt phẳng. Hai mặt phẳng vuông góc
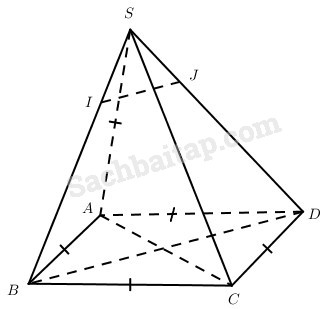
Cho hình chóp S.ABCD có đáy là hình thoi, cạnh bên SA = AB và SA vuông góc với BC.
a) Tính góc giữa hai đường thẳng SD và BC
b) Gọi I, J lần lượt là các điểm thuộc SB và SD sao cho IJ // BD. Chứng minh rằng góc giữa AC và IJ không phụ thuộc vào vị trí của I và J.
Advertisements (Quảng cáo)
a) Vì BC // AD nên góc giữa SD và BC bằng góc giữa SD và AD.
Từ giả thiết, ta có \(SA \bot BC\) nên \(SA \bot A{\rm{D}}\) mặt khác SA bằng cạnh của hình thoi ABCD, nên \(\widehat {S{\rm{D}}A} = {45^0}\) là góc phải tìm.
Vậy góc giữa BC và SD bằng 45°.
b) Do ABCD là hình thoi nên \(AC \bot B{\rm{D}}\) . Mặt khác IJ // BD nên \(AC \bot IJ\) tức là góc giữa IJ và AC bằng 90° không đổi.