Cho tứ diện ABCD. Gọi I, J, H, K, E, F lần lượt là trung điểm của các cạnh AB, CD, BC, AD, AC, BD. Chứng minh rằng
\(A{B^2} + C{{\rm{D}}^2} + A{C^2} + B{{\rm{D}}^2} + B{C^2} + A{{\rm{D}}^2} \)
\(= 4\left( {I{J^2} + H{K^2} + E{F^2}} \right)\)

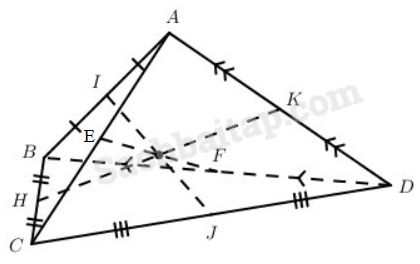
Trước hết, ta chứng minh
\(A{C^2} + B{{\rm{D}}^2} + B{C^2} + A{{\rm{D}}^2} = A{B^2} + C{{\rm{D}}^2} + 4I{J^2}\)
Đặt \(\overrightarrow {DA} = \overrightarrow a ,\overrightarrow {DB} = \overrightarrow b ,\overrightarrow {DC} = \overrightarrow c \)
Ta có:
\(\eqalign{ & \overrightarrow {IJ} = \overrightarrow {IA} + \overrightarrow {AD} + \overrightarrow {DJ} \cr & = - {{\overrightarrow {AB} } \over 2} + \overrightarrow {AD} + {{\overrightarrow {DC} } \over 2} \cr & = - {1 \over 2}\left( { - \overrightarrow a + \overrightarrow b } \right) + \left( { - \overrightarrow a } \right) + \left( {{{\overrightarrow c } \over 2}} \right) \cr & = {{ - \overrightarrow a - \overrightarrow b + \overrightarrow c } \over 2} \cr & {\overrightarrow {AB} ^2} + {\overrightarrow {CD} ^2} + 4{\overrightarrow {IJ} ^2} \cr & = {\left( {\overrightarrow b - \overrightarrow a } \right)^2} + {\overrightarrow c ^2} + {\left( {\overrightarrow a + \overrightarrow b - \overrightarrow c } \right)^2} \cr & = 2{\overrightarrow b ^2} + 2{\overrightarrow a ^2} + 2{\overrightarrow c ^2} - 2\overrightarrow a .\overrightarrow c - 2\overrightarrow b .\overrightarrow c \cr & {\overrightarrow {AC} ^2} + {\overrightarrow {BD} ^2} + {\overrightarrow {BC} ^2} + {\overrightarrow {AD} ^2} \cr & = {\left( {\overrightarrow c - \overrightarrow a } \right)^2} + {\overrightarrow b ^2} + {\left( {\overrightarrow c - \overrightarrow b } \right)^2} + {\overrightarrow a ^2} \cr & = 2{\overrightarrow a ^2} + 2{\overrightarrow b ^2} + 2{\overrightarrow c ^2} - 2\overrightarrow a .\overrightarrow c - 2\overrightarrow b .\overrightarrow c \cr} \)
Vậy, ta có:
Advertisements (Quảng cáo)
\(A{C^2} + B{{\rm{D}}^2} + B{C^2} + A{{\rm{D}}^2} = A{B^2} + C{{\rm{D}}^2} + 4I{J^2}\)
Tương tự, ta có:
\(A{C^2} + B{{\rm{D}}^2} + A{B^2} + C{{\rm{D}}^2}\)
\(= B{C^2} + A{{\rm{D}}^2} + 4H{K^2}\)
\( A{B^2} + C{{\rm{D}}^2} + B{C^2} + A{{\rm{D}}^2} \)
\(= A{C^2} + B{D^2} + 4E{F^2} \)
Từ đó suy ra:
\(A{B^2} + C{{\rm{D}}^2} + A{C^2} + B{{\rm{D}}^2} + B{C^2} + A{{\rm{D}}^2}\)
\(= 4\left( {I{J^2} + H{K^2} + E{F^2}} \right)\)
