Advertisements (Quảng cáo)
Cho tứ diện ABCD. Gọi I, J, H, K lần lượt là trung điểm của BC, AC, AD, BD. Hãy tính góc giữa hai đường thẳng AB và CD trong các trường hợp sau:
a) Tứ giác IJHK là hình thoi có đường chéo \(IH = \sqrt 3 IJ\).
b) Tứ giác IJHK là hình chữ nhật
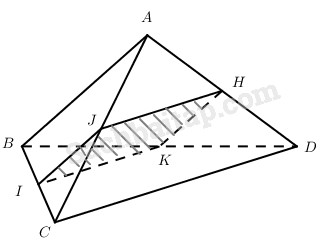
Góc giữa hai đường thẳng AB và CD bằng góc giữa hai đường thẳng IJ và IK, đó là góc \(\widehat {JIK}\) hoặc \({180^0} – \widehat {JIK}\).
a) Vì hình tứ giác IJHK là hình thoi mà \(IH = \sqrt 3 IJ\), nên từ \(I{K^2} + I{H^2} = 4I{J^2}\).
Advertisements (Quảng cáo)
ta có: \(I{K^2} = I{J^2}\)
hay IK = IJ
Như vậy JIK là tam giác đều, do đó \(\widehat {JIK} = {60^0}\).
Vậy góc giữa AB và CD trong trường hợp này bằng 60°.
b) Khi tứ giác IJHK là hình chữ nhật thì \(\widehat {JIK} = {90^0}\). Do đó, góc giữa AB và CD bằng 90°.