Trong mặt phẳng (P) cho đường tròn (C) đường kính AC = 2R. Gọi H là điểm thuộc AC (0 < AH < 2R). Một đường thẳng ∆ đi qua H cắt đường tròn (C) tại hai điểm B và D. Gọi S là điểm cố định sao cho SA vuông góc với (P), đặt SA = h. Một mặt phẳng (Q) đi qua điểm A và vuông góc với SC cắt các đường thẳng SB, SC, SD, SH lần lượt tại các điểm B1, C1, D1, H1.
a) Chứng minh rằng tứ giác AB1C1D1 nôi tiếp một đường tròn.
b) Đường thẳng ∆ phải thỏa mãn điều kiện gì để H1 là trung điểm của B1D1?
c) Đường thẳng ∆ phải thỏa mãn điều kiện gì để AB1C1D1 là hình vuông?

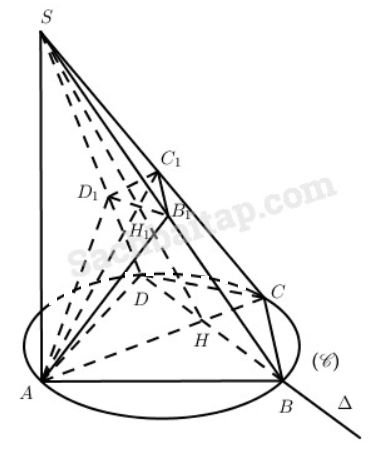
a) Vì (Q) qua A và \(\left( Q \right) \bot SC\) nên \(A{B_1} \bot SC\).
Mặt khác dễ thấy \(BC \bot \left( {SAB} \right)\) nên \(BC \bot A{B_1}\).
Vậy \(A{B_1} \bot mp\left( {SBC} \right)\), tức là \(A{B_1} \bot {B_1}{C_1}\).
Tương tự như trên, ta có \(A{{\rm{D}}_1} \bot {D_1}{C_1}.\)
Do đó, tứ diện AB1C1D1 nội tiếp đường tròn.
b)
Do tứ giác AB1C1D1 nội tiếp đường tròn đường kính AC1 mà AC1 cắt B1D1, tại H1 nên H1 là trung điểm của B1D1, khi đó xảy ra một trong hai trường hợp sau:
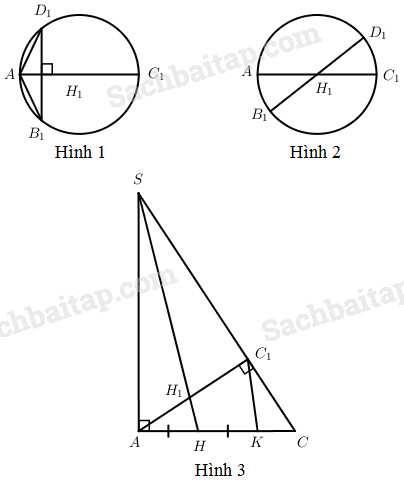
- Trường hợp 1: \({B_1}{D_1} \bot A{C_1}\) tại H1 (Hình 1)
- Trường hợp 2: B1D1 qua trung điểm H1 của AC1 (Hình 2)
Advertisements (Quảng cáo)
Xét trường hợp 1
Vì \({B_1}{D_1} \bot A{C_1}\) nên \(A{B_1} = A{{\rm{D}}_1}\)
Mặt khác \(A{B_1},A{{\rm{D}}_1}\) là hai đường cao của hai tam giác vuông SAB và SAD nên
\(A{B_1} = A{{\rm{D}}_1} \Leftrightarrow AB = A{\rm{D}}\)
(Vì \({1 \over {A{S^2}}} + {1 \over {A{B^2}}} = {1 \over {AB_1^2}}\) và \({1 \over {A{S^2}}} + {1 \over {A{D^2}}} = {1 \over {AD_1^2}}\))
Lại có AC là đường kính của (C) nên
\(AB = A{\rm{D}} \Leftrightarrow {\rm{BD}} \bot AC\).
Vậy nếu đường thẳng ∆ vuông góc với AC tại H mà 0 < AH < AC thì H1 là trung điểm của B1D1.
Xét trường hợp 2 (Hình 3)
Kẻ C1K // H1H, do H1 là trung điểm của AC1 nên AH = HK = x, từ đó CK = 2R – 2x. Khi đó
\(\eqalign{ & {{2{\rm{R}} - 2{\rm{x}}} \over {2{\rm{R}} - x}} = {{CK} \over {CH}} = {{C{C_1}} \over {C{\rm{S}}}} \cr & = {{C{C_1}.C{\rm{S}}} \over {C{{\rm{S}}^2}}} = {{A{C^2}} \over {C{{\rm{S}}^2}}} = {{4{{\rm{R}}^2}} \over {{h^2} + 4{R^2}}} \cr & \Leftrightarrow \left( {R - x} \right)\left( {{h^2} + 4{{\rm{R}}^2}} \right) = 2{R^2}\left( {2{\rm{R}} - x} \right) \cr & \Leftrightarrow x = {{R{h^2}} \over {{h^2} + 2{{\rm{R}}^2}}} \cr} \)
Dễ thấy 0 < x < 2R
Vậy nếu đường thẳng ∆ quay quanh điểm H mà H được xác định bởi
\(AH = x = {{R{h^2}} \over {{h^2} + 2{{\rm{R}}^2}}},H \in AC\)
thì H1 là trung điểm của B1D1
