Cho hình chóp S.ABCD có đáy là hình thoi, đường chéo AC = 4a, đường chéo BD = 2a; O là giao điểm của AC với BD và SO vuông góc với mặt phẳng (ABC), SO = h. Một mặt phẳng (α) đi qua điểm A và vuông góc với đường thẳng SC tại điểm C1. Tìm hệ thức liên hệ giữa a và h để điểm C1 nằm trong đoạn thẳng SC, C1 khác S và khác C. Khi đó, tính diện tích thiết diện của hình chóp S.ABCD cắt bởi mp(α).

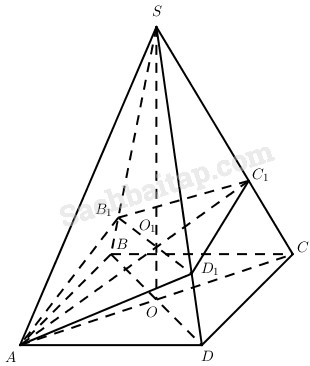
Vì \(\left( \alpha \right) \bot SC\) và \(A \in \left( \alpha \right)\) nên \(A{C_1} \bot SC\). Mặt khác, gọi \({B_1}{D_1} = \left( \alpha \right) \cap \left( {SBD} \right)\) thì B1D1 song song với BD và B1D1 qua \({O_1} = A{C_1} \cap SO\) (do \(B{\rm{D}} \bot SC,\left( \alpha \right) \bot SC\) nên BD // (α)).
Vì SAC là tam giác cân tại S và \(A{C_1} \bot SC\) nên C1 thuộc SC khi và chỉ khi \(\widehat {ASC} < {90^0}\) tức là \(\widehat {OSC} < {45^0}\). Xét tam giác vuông SOC, điều kiện \(\widehat {OSC} < {45^0}\) tương đương với \(SO > OC = {{AC} \over 2} = 2a\). Vậy để C1 thuộc SC, C1 không trùng với C và S thì hệ thức liên hệ giữa h và a là h > 2a.
Dễ thấy thiết diện của S.ABCD khi cắt bởi (α) là tứ giác AB1C1D1 có tính chất \(A{C_1} \bot {B_1}{D_1}\) . Do đó \({S_{A{B_1}{C_1}{D_1}}} = {1 \over 2}A{C_1}.{B_1}{D_1}\).
Ta có:
\(\eqalign{ & A{C_1}.SC = SO.AC \Rightarrow A{C_1} = {{4{\rm{a}}h} \over {\sqrt {4{{\rm{a}}^2} + {h^2}} }}; \cr & {{{B_1}{D_1}} \over {B{\rm{D}}}} = {{S{O_1}} \over {SO}}, \cr} \)
Advertisements (Quảng cáo)
mặt khác
\(\eqalign{ & {{{O_1}O} \over {CO}} = {{AO} \over {SO}} \cr & \Rightarrow {O_1}O = {{4{{\rm{a}}^2}} \over h} \cr & \Rightarrow S{O_1} = {{{h^2} - 4{a^2}} \over h} \cr} \)
Từ đó \({{{B_1}{D_1}} \over {B{\rm{D}}}} = {{{h^2} - 4{{\rm{a}}^2}} \over {{h^2}}}\)
hay \({B_1}{D_1} = {{2{\rm{a}}\left( {{h^2} - 4{{\rm{a}}^2}} \right)} \over {{h^2}}}\)
Vậy
\(\eqalign{ & {S_{A{B_1}{C_1}{D_1}}} = {1 \over 2}.{{4{\rm{a}}h} \over {\sqrt {4{{\rm{a}}^2} + {h^2}} }}.{{2{\rm{a}}\left( {{h^2} - 4{{\rm{a}}^2}} \right)} \over {{h^2}}} \cr & = {{4{{\rm{a}}^2}\left( {{h^2} - 4{{\rm{a}}^2}} \right)} \over {h\sqrt {4{{\rm{a}}^2} + {h^2}} }} \cr} \)
