Cho tam giác đều ABC có cạnh bằng a. Gọi ∆ là đường thẳng vuông góc với mặt phẳng (ABC) kẻ từ A. Với điểm M bất kì thuộc ∆, \(M ≢ A\), gọi K là trực tâm của tam giác MBC và ∆1 là đường thẳng đi qua K và vuông góc với mặt phẳng (MBC). Chứng minh rằng:
a) ∆1 đi qua điểm cố định khi M thay đổi trên ∆.
b) ∆1 cắt ∆ tại điểm N và BM vuông góc với CN, CM vuông góc với BN. Xác định vị trí điểm M để độ dài MN đạt giá trị bé nhất.

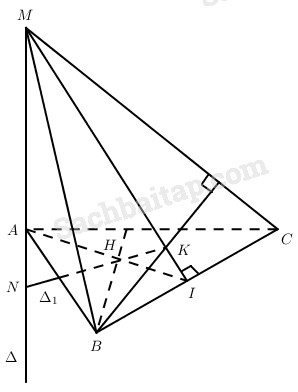
a) Gọi I là trung điểm của BC thì \(AI \bot BC,MI \bot BC\). Vậy K thuộc MI. Ta cũng có \(BC \bot \left( {MAI} \right)\). Do ∆1 đi qua K và \({\Delta _1} \bot \left( {MBC} \right)\) nên \({\Delta _1} \bot BC\). Vậy ∆1 nằm trong mp(MAI). Gọi giao điểm của ∆1 với AI là H thì \(HK \bot MC\), mặt khác \(BK \bot MC\), từ đó MC vuông góc với (BHK) hay \(MC \bot BH\).
Từ \(\Delta \bot \left( {ABC} \right),\,BH \bot MC\) nên \(BH \bot AC\).
Vậy H là trực tâm của tam giác ABC. Điều này chứng tỏ khi M thay đổi trên \(\Delta\) thì \(\Delta_1\) đi qua điểm cố định là trực tâm H của tam giác ABC.
b) Vì ∆1 là đường thăngt HK nên ∆1 cắt ∆ tại điểm N.
Advertisements (Quảng cáo)
Theo câu a), ta có MC vuông góc với (BHK) mà BN thuộc mặt phẳng này, vậy NB vuông góc với MC.
Tương tự như trên, ta cũng có \(MB \bot NC\)
Từ ∆AHN đồng dạng ∆AMI, ta có \({{AH} \over {AM}} = {{AN} \over {AI}} \Rightarrow AH.AI = AM.AN\)
Mặt khác \(AH.AI = {{a\sqrt 3 } \over 3}.{{a\sqrt 3 } \over 2} = {{{a^2}} \over 2}\) .
do đó \(AM.AN = {{{a^2}} \over 2}\)
Ta có: MN = AM + AN
Vậy MN ngắn nhất khi và chỉ khi \(AM = AN = {{a\sqrt 2 } \over 2}\).
Hệ thức này xác định điểm M để MN có độ dài ngắn nhất.
