42. Trang 11 Sách bài tập Hình Học 11 nâng cao.
Cho hai phép quay \({Q_A}\) và \({Q_B}\) có tâm quay là A và B (phân biệt) và có cùng góc quay \({90^o}.\) Gọi F là hợp thành của \({Q_A}\) và \({Q_B}\), F’ là hợp thành của \({Q_B}\) và \({Q_A}\). Hãy chứng tỏ rằng F và F’ là những phép đối xứng tâm và nêu rõ cách xác định tâm đối xứng của phép đó.

Advertisements (Quảng cáo)
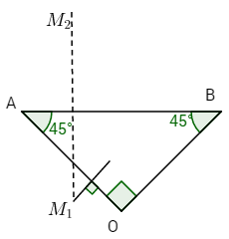
Lấy điểm O sao cho tam giác OAB là tam giác vuông cân với góc \(\left( {OA,AB} \right) = \left( {BA,BO} \right) = {45^o}.\) Khi đó, \({Q_A}\) là hợp thành của hai phép đối xứng trục \({Đ_{AO}}\) và \({Đ_{AB}},\) còn \({Q_B}\) là hợp thành của hai phép đối xứng trục \({Đ_{AB}}\) và \({Đ_{BO}}.\) Vậy F là hợp thành của bốn phép đối xứng trục theo thứ tự: \({Đ_{AO}},\,{Đ_{AB}},\,{Đ_{AB}},\,{Đ_{BO}},\) tức cũng là hợp thành của hai phép đối xứng trục \({Đ_{AO}}\) và \({Đ_{BO}}.\) Vì AO đối xứng qua điểm O. Chú ý rằng có thể xác định điểm O bởi điều kiện: Tam giác OAB vuông cân \(\left( {OB,OA} \right) = {90^o}.\)
Tương tự F là phép đối xứng qua tâm O’, sao cho O’AB là tam giác vuông cân mà \(\left( {OA,OB} \right) = {90^o}.\)
