Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến ∆ và tạo với nhau góc α. Xét hai điểm M và N lần lượt thuộc (P) và (Q). Kẻ MI vuông góc với ∆, NJ vuông góc với ∆. Cho biết \(MI = a,NJ = b,IJ = c\). Tính độ dài MN.

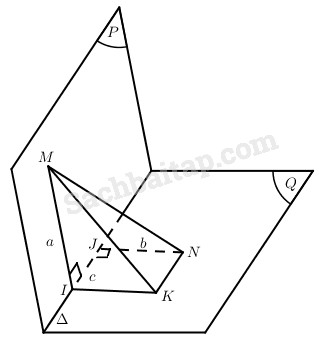
Trong mp(Q), kẻ qua I đường thẳng song song với JN và kẻ qua N đường thẳng song song với IJ, chúng cắt nhau tại K.
Dễ thấy \(MI \bot NK\), tứ giác IJNK là hình chữ nhật.
Như vậy \(MI \bot NK,IK \bot KN\), từ đó \(MK \bot KN\), ngoài ra IK = b, NK = c.
Vì MI và IK cũng vuông góc với IJ.
Advertisements (Quảng cáo)
Vậy \(\widehat {MIK}\) hoặc \({180^0} - \widehat {MIK}\) là góc giữa hai mặt phẳng (P) và (Q).
Ta có:
\(\eqalign{ & M{N^2} = M{K^2} + K{N^2} = M{K^2} + {c^2}; \cr & M{K^2} = {a^2} + {b^2} - 2ab\cos \widehat {MIK} \cr} \)
Vậy \(MN = \sqrt {{a^2} + {b^2} - 2{\rm{a}}b\cos \widehat {MIK} + {c^2}} \)
hoặc \(MN = \sqrt {{a^2} + {b^2} + 2{\rm{a}}b\cos \widehat {MIK} + {c^2}} \).
