63. Trang 62 Sách Bài tập Hình học 11 Nâng cao
Cho hai đường thẳng d và d’ chéo nhau.Trên d đặt hai đoạn thẳng liên tiếp bằng nhau AB và BC (B ở giữa A và C); trên d’ đặt hai đoạn thẳng liên tiếp cũng bằng nhau A’B’ và B’C’ (B’ ở giữa A’ và C’). Chứng minh rằng AA’ + CC’ > 2 BB’.

Advertisements (Quảng cáo)
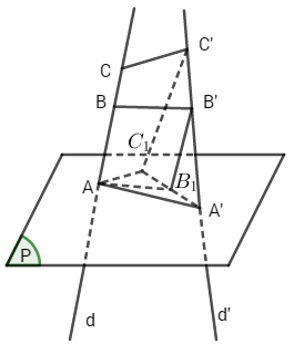
Gọi (P) là mặt phẳng đi qua AA’ và song song với BB’. Theo định lí Ta-lét, ta cũng có CC’ // mp(P). Xét phép chiếu song song lên mp(P) theo phương chiếu d, ta được hình chiếu của A’, B’, C’ tương ứng là A’, B1, C1. Khi đó ba điểm A’, B1, C1 thẳng hàng. Ta có C’C1 // CA và vì CC’ // mp(P) nên giao tuyến AC1 của mp(CC’C1A) với mp(P) song song với CC’. Do đó tứ giác CC’C1A là hình bình hành, nên AC1 = CC’. Tương tự như vậy, ta cũng chứng minh được AB1 = BB’. Ta phải chứng minh AA’ +AC1 > 2AB1.
Thật vậy, vì B’ là trung điểm của A’C’ nên B1 là trung điểm của cạnh A’C1 của tam giác AA’C1. Từ đó dễ thấy tổng của hai cạnh AA’ và AC1 trong tam giác AA’C1 lớn hơn hai lần trung tuyến ứng với cạnh thứ ba.
