64. Trang 62 Sách Bài tập Hình học 11 Nâng cao
Cho hình hộp ABCD.A’B’C’D’. Gọi M, N lần lượt là trung điểm của CD và CC’.
a) Xác định đường thẳng qua M cắt AN và cắt A’B.
b) Gọi I, J lần lượt là giao điểm của \(\Delta \) với AN và A’B. Hãy tìm tỉ số \({{IM} \over {{\rm{IJ}}}}\).

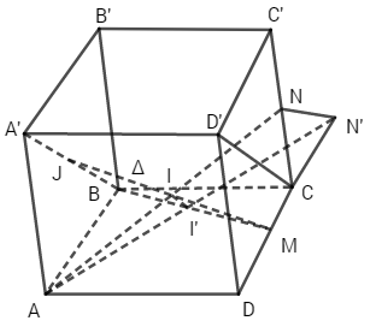
a) Giả sử đã dựng được đường thẳng \(\Delta \) cần tìm cắt cả AN và BA’. Gọi I, J lần lượt là giao điểm của \(\Delta \) với AN và BA’.
Xét phép chiếu song song lên mp(ABCD) theo phương chiếu A’B. Khi đó ba điểm I, J, M lần lượt có hình chiếu là B, I’ và M. Do đó ba điểm B, I’, M thẳng hàng. Gọi N’ là hình chiếu của N thì AN’ là hình chiếu của AN. Vì I thuộc AN nên I’ thuộc AN’. Vậy I’ là giao điểm của BM và AN’.
Từ phân tích ở trên ta có thể dựng đường thẳng \(\Delta \) theo các bước sau đây:
Advertisements (Quảng cáo)
- Lấy giao điểm I’ của AN’ và BM.
- Trong mp(ANN’) dựng II’ // NN’ (đã có NN’ // CD’) cắt AN tại I.
- Vẽ đường thẳng MI, đó là đường thẳng \(\Delta \) cần tìm.
Dễ chứng minh được, đường thẳng \(\Delta \) nói trên cắt BA’.
b) Dễ thấy: MC = CN’
suy ra: MN’ = CD = AB.
Do đó I’ là trung điểm của BM.
Mặt khác II’ // JB, nên II’ là đường trung bình của tam giác MBJ, suy ra:
\(IM = {\rm{IJ}} \Rightarrow {{IM} \over {IJ}} = 1\)
