73. Trang 64 Sách bài tập Hình học 11 nâng cao.
Cho hình chóp S.ABCD có đáy là hình bình hành. Một mặt phẳng (P) lần lượt cắt các cạnh SA, SB, SC tại A’, B’, C’. Gọi O là giao điểm của AC và BD; I là giao điểm của A’C’ và SO.
a) Tìm giao điểm D’ của mp(P) với cạnh SD.
b) Chứng minh rằng \({{SA} \over {SA’}} + {{SC} \over {SC’}} = {{2SO} \over {SI}}\)
c) Chứng minh rằng \({{SA} \over {SA’}} + {{SC} \over {SC’}} = {{SB} \over {SB’}} + {{SD} \over {SD’}}.\)

a) Trong mp(SAC) nối A’ với C’ cắt SO tại I. Trong mp(SBD) nối B’ với I cắt SD tại D’. Khi đó D’ chính là giao điểm của mp(P) với SD.
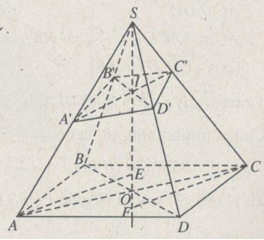
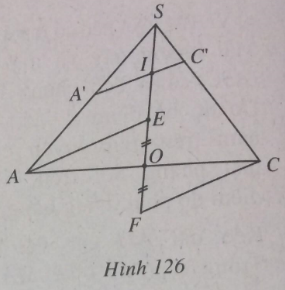
b) (h.126)
Advertisements (Quảng cáo)
Trong mp(SAC), kẻ AE // A’C’ cắt SO tại E; kẻ CF // A’C’ cắt SO tại F. Ta có:
\({{SA} \over {SA’}} = {{SE} \over {SI}} = {{SO - OE} \over {SI}}\,\,\,\,(1)\)
\({{SC} \over {SC’}} = {{SF} \over {SI}} = {{SO + \,OF} \over {SI}}\,\,\,\,(2)\)
Do O là trung điểm của AC và AE // CF, nên OE = OF.
Vậy từ (1) và (2), suy ra \({{SA} \over {SA’}} + {{SC} \over {SC’}} = {{2SO} \over {SI}}\) (3)
c) Chứng minh tương tự câu b), ta có:
\({{SB} \over {SB’}} + {{SD} \over {SD’}} = {{2SO} \over {SI}}\) (4)
Từ (3) và (4), suy ra:
\({{SA} \over {SA’}} + {{SC} \over {SC’}} = {{SB} \over {SB’}} + {{SD} \over {SD’}}.\)
