Cho tứ diện ABCD. Chứng minh rằng:
a) Nếu ABCD là hình chữ nhật thì với mọi điểm M trog không gian ta luôn có \(M{A^2} + M{C^2} = M{B^2} + M{{\rm{D}}^2}\) .
b) Nếu ABCD là hình bình hành thì \(M{A^2} + M{C^2} - M{B^2} - M{{\rm{D}}^2}\) không phụ thuộc vào vị trí điểm M trong không gian. Điều ngược lại có đúng không?

a) Cách 1. Gọi O là giao điểm của AC và BD
\(\eqalign{ & M{A^2} + M{C^2} = 2M{O^2} + {{A{C^2}} \over 2} \cr & M{B^2} + M{{\rm{D}}^2} = 2M{O^2} + {{B{{\rm{D}}^2}} \over 2} \cr} \)
Vì ABCD là hình chữ nhật nên AC = BD. Vậy \(M{A^2} + M{C^2} = M{B^2} + M{{\rm{D}}^2}\).
Cách 2.
\(\eqalign{& M{A^2} + M{C^2} = {\left( {\overrightarrow {MO} + \overrightarrow {OA} } \right)^2} + {\left( {\overrightarrow {MO} + \overrightarrow {OC} } \right)^2} \cr & = 2\overrightarrow {M{O^2}} + 2\overrightarrow {MO} .\left( {\overrightarrow {OA} + \overrightarrow {OC} } \right) + {\overrightarrow {OA} ^2} + {\overrightarrow {OC} ^2} \cr & = 2\left( {M{O^2} + O{A^2}} \right) \cr & \left( {do\,OA = OC,\overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow 0 } \right) \cr} \)
Tương tự như tên ta có \(M{B^2} + M{{\rm{D}}^2} = 2\left( {M{O^2} + O{B^2}} \right)\).
Vì ABCD là hình chữ nhật nên OA = OB. Vậy \(M{A^2} + M{C^2} = M{B^2} + M{{\rm{D}}^2}\).
b) Gọi I, J lần lượt là trung điểm của AC cà BD, khi đó:
\(\eqalign{ & M{A^2} + M{C^2} - M{B^2} - M{{\rm{D}}^2} \cr & = {\left( {\overrightarrow {MI} + \overrightarrow {IA} } \right)^2} + {\left( {\overrightarrow {MI} + \overrightarrow {IC} } \right)^2} - {\left( {\overrightarrow {MJ} + \overrightarrow {JB} } \right)^2} - {\left( {\overrightarrow {MJ} + \overrightarrow {J{\rm{D}}} } \right)^2} \cr & = 2M{I^2} + I{A^2} + I{C^2} - 2M{J^2} - I{B^2} - J{{\rm{D}}^2} \cr & = 2\left( {M{I^2} - M{J^2}} \right) + {1 \over 2}\left( {A{C^2} - B{{\rm{D}}^2}} \right) \cr} \)
Advertisements (Quảng cáo)
● Nếu ABCD là hình bình hành thì I ≡ J
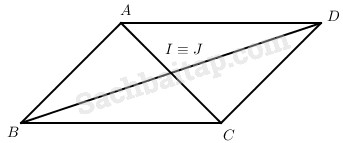
Khi đó
\(\eqalign{ & M{A^2} + M{C^2} - M{B^2} - M{{\rm{D}}^2} \cr & = {1 \over 2}\left( {A{C^2} - B{{\rm{D}}^2}} \right) \cr} \)
tức là \(M{A^2} + M{C^2} - M{B^2} - M{{\rm{D}}^2}\) không phụ thuộc vào vị trí của điểm M.
● Ngược lạ, nếu \(M{A^2} + M{C^2} - M{B^2} - M{{\rm{D}}^2}\) không phụ thuộc vào bị trí của điểm M thì \(M{I^2} - M{J^2}\) cũng là hằng số. Khi đó chọn M lần lượt là điểm I và điểm J thì \(I{I^2} - I{J^2} = J{I^2} - J{J^2}\) , suy ra \( - I{J^2} = I{J^2}\), tức là IJ = 0 hay I ≡ J
Vậy ABCD là hình bình hành.
Chú ý cũng có thể sử dụng các công thức:
\(\eqalign{ & M{A^2} + M{C^2} = 2M{I^2} + {{A{C^2}} \over 2} \cr & M{B^2} + M{D^2} = 2M{J^2} + {{B{D^2}} \over 2} \cr} \)
và từ đó ta có
\(\eqalign{ & M{A^2} + M{C^2} - M{B^2} - M{{\rm{D}}^2} \cr & = 2\left( {M{I^2} - M{J^2}} \right) + {1 \over 2}\left( {A{C^2} - B{{\rm{D}}^2}} \right) \cr} \)
rồi lí luận như trên để đi đến kết quả.
