Chứng minh rằng mỗi phép quay đều có thể xem là kết quả của việc thực hiện liên tiếp hai phép đối xứng trục.

Advertisements (Quảng cáo)
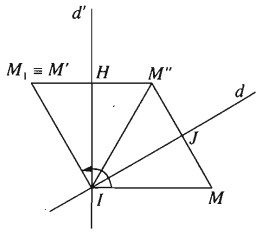
Gọi \({Q_{\left( {I,\alpha } \right)}}\) là phép quay tâm I góc \(\alpha \) . Lấy đường thẳng d bất kì qua I. Gọi d’ là ảnh của d qua phép quay tâm I góc \({\alpha \over 2}\). Lấy điểm M bất kì và gọi \(M’ = {Q_{\left( {I,\alpha } \right)}}\left( M \right)\). Gọi M” là ảnh của M qua phép đối xứng qua trục d. \(M_1\) là ảnh của M” qua phép đối xứng qua trục d’. Gọi J là giao của MM” với d, H là giao của \(M”{M_1}\) với d’. Khi đó ta có đẳng thức giữa các góc lượng giác sau:
\(\eqalign{
& \left( {IM,I{M_1}} \right) = \left( {IM,IM”} \right) + \left( {IM”,I{M_1}} \right) \cr
& = 2\left( {IJ,IM”} \right) + 2\left( {IM”,IH} \right) \cr
& = 2\left( {IJ,IH} \right) \cr
& = 2{\alpha \over 2} = a = \left( {IM,IM’} \right) \cr} \)
Từ đó suy ra \(M’ \equiv {M_1}\). Như vậy M’ có thể xem là ảnh của sau khi thực hiện liên tiếp hai phép đối xứng qua hai trục d và d’.
