Dãy số \(\left( {{x_n}} \right)\) được biểu diễn trên trục số bởi tập hợp các điểm, kí hiệu là A :
$$A = \left\{ {{A_0},{A_1},{A_2}..{A_n}} \right\}$$
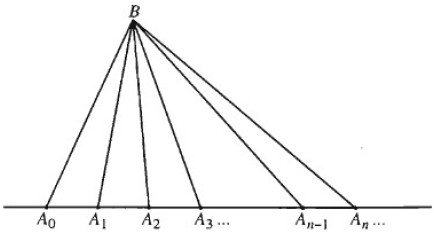
Gọi B là điểm nằm ngoài trục số. Người ta dựng các tam giác đỉnh B và hai đỉnh còn lại thuộc tập hợp A.
Đặt un là số các tam giác được tạo thành từ B và hai trong số n + 1 điểm \({A_0},{A_1},{A_2}..{A_n}\) rồi lập dãy số un
a) Tính \({u_1},{u_2},{u_3},{u_4}\) ;
b) Chứng minh rằng \({u_n} = C_{n + 1}^2\) và \9{u_{n + 1}} = {u_n} + n + 1\)

Advertisements (Quảng cáo)
a)
\(\eqalign{
& {u_1} = 1 \cr
& {u_2} = 3 \cr
& {u_3} = 6 \cr
& {u_4} = 10 \cr} \)
b) Số các tam giác un tạo thành từ B và n + 1 điểm chính là số tổ hợp chập 2 của n + 1 phần tử:
Áp dụng công thức \(C_n^k = C_{n - 1}^k + C_{n - 1}^{k - 1}\)
Ta có \(C_{n + 2}^2 = C_{n + 1}^2 + C_{n + 1}^1\)
Hay \({u_{n + 1}} = {u_n} + n + 1\)
