Khi mặt phẳng (AA’C’C) vuông góc với mặt phẳng (BB’D’D)?. Bài 3.22 trang 152 Sách bài tập (SBT) Hình học 11 - Bài 4. Hai mặt phẳng vuông góc
Hình hộp ABCD.A’B’C’D’ có tất cả các cạnh đều bằng nhau. Chứng minh rằng \(AC \bot B’D’,AB’ \bot C{\rm{D}}’\) và \(A{\rm{D}}’ \bot CB’\). Khi mặt phẳng (AA’C’C) vuông góc với mặt phẳng (BB’D’D)?

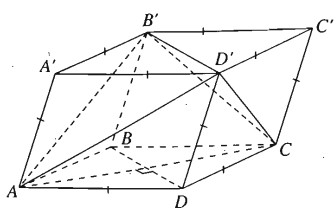
Theo giả thiết các mặt của hình hộp đều là hình thoi.
Advertisements (Quảng cáo)
Ta có ABCD là hình thoi nên \(AC \bot B{\rm{D}}\)
Theo tính chất của hình hộp: \(B{\rm{D}}\parallel B’D’\),do đó \(AC \bot B'{\rm{D’}}\).
Chứng minh tương tự ta được \(AB’ \bot C{\rm{D’, AD}}’ \bot CB’\)
Hai mặt phẳng (AA’C’C) và (BB’D’D) vuông góc với nhau khi hình hộp ABCD.A’B’C’D’là hình lập phương.
