
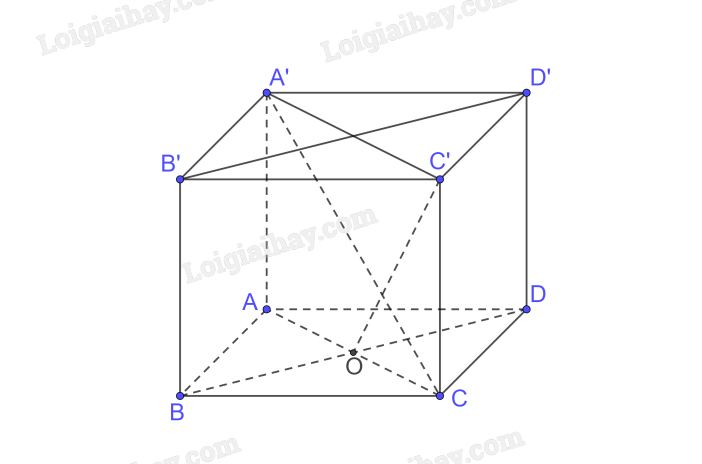
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a.
a) Tính độ dài đường chéo của hình lập phương.
b) Chứng minh rằng (ACC′A′) \( \bot \) (BDD′B′).
c) Gọi O là tâm của hình vuông ABCD. Chứng minh rằng \(\widehat {COC’}\) là một góc phẳng của góc nhị diện [C, BD, C’]. Tính (gần đúng) số đo của các góc nhị diện [C, BD, C’], [A, BD, C’].

- Hai mặt phẳng được gọi là vuông góc nếu một đường thẳng nằm trong mặt phẳng này vuông góc với mặt phẳng kia.
- Từ một điểm O bất kì thuộc cạnh a của góc nhị diện [P, a, Q], vẽ các tia Ox, Oy tương ứng thuộc (P), (Q) và vuông góc với a. Góc xOy được gọi là một góc phẳng của góc nhị diện [P, a, Q].

a) Xét tam giác ABC vuông tại B có
Advertisements (Quảng cáo)
\(A{C^2} = A{B^2} + B{C^2} = {a^2} + {a^2} = 2{a^2} \Rightarrow AC = a\sqrt 2 \)
Xét tam giác AA’C vuông tại A có
\(A'{C^2} = A{A’^2} + A{C^2} = {a^2} + {\left( {a\sqrt 2 } \right)^2} = 3{a^2} \Rightarrow A’C = a\sqrt 3 \)
Vậy độ dài đường chéo hình lập phương bằng \(a\sqrt 3 \)
b) Ta có \(\begin{array}{l}BD \bot AC,BD \bot AA’ \Rightarrow BD \bot \left( {ACC’A’} \right);BD \subset \left( {BDD’B’} \right)\\ \Rightarrow \left( {ACC’A’} \right) \bot \left( {BDD’B’} \right)\end{array}\)
c) Ta có \(C’O \bot BD\left( {BD \bot \left( {ACC’A’} \right)} \right),CO \bot BD \Rightarrow \left[ {C,BD,C’} \right] = \left( {CO,C’O} \right) = \widehat {COC’}\)
\(OC = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2}\)
Xét tam giác COC’ vuông tại C có
\(\tan \widehat {COC’} = \frac{{CC’}}{{OC}} = \frac{a}{{\frac{{a\sqrt 2 }}{2}}} = \sqrt 2 \Rightarrow \widehat {COC’} = \arctan \sqrt 2 \)
Ta có \(C’O \bot BD\left( {BD \bot \left( {ACC’A’} \right)} \right),AO \bot BD \Rightarrow \left[ {A,BD,C’} \right] = \left( {AO,C’O} \right) = \widehat {AOC’}\)
\(\widehat {AOC’} = {180^0} - \widehat {COC’} \approx 125,{26^0}\)
