
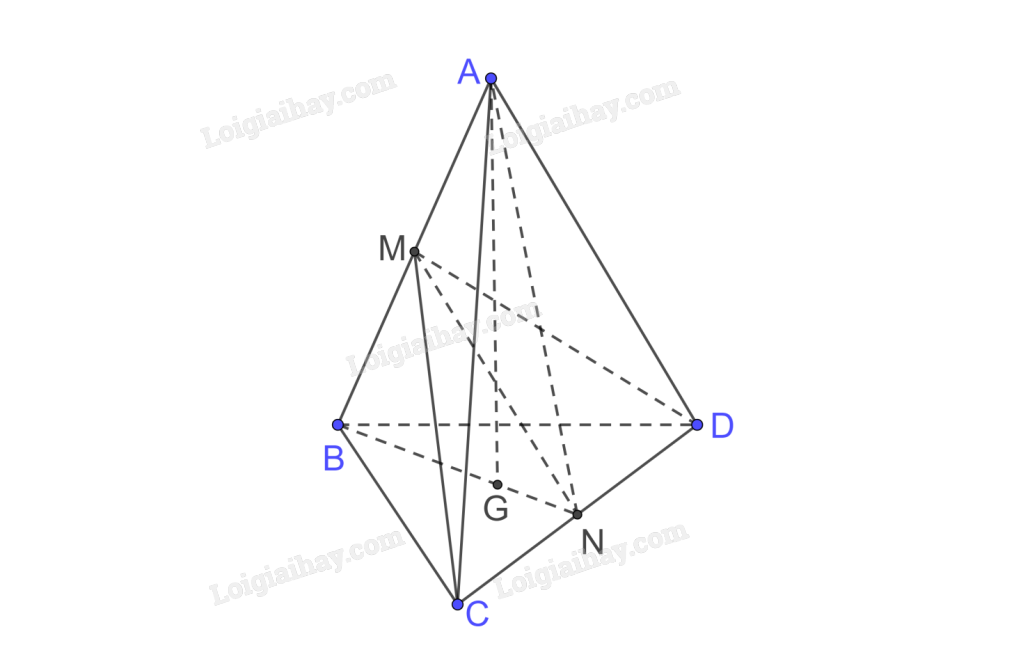
Cho tứ diện ABCD có các cạnh đều bằng a. Gọi M, N tương ứng là trung điểm của các cạnh AB, CD. Chứng minh rằng:
a) MN là đường vuông góc chung của AB và CD.
b) Các cặp cạnh đối diện trong tứ diện ABCD đều vuông góc với nhau.

Hai đường thẳng vuông góc nếu đường thẳng này vuông góc với mặt phẳng chứa đường thẳng kia.

Advertisements (Quảng cáo)
a) Ta có \(BN \bot CD,AG \bot CD \Rightarrow CD \bot \left( {ABN} \right),MN \subset \left( {ABN} \right) \Rightarrow CD \bot MN\)
Vì BN, AN lần lượt là 2 đường trung tuyến của 2 tam giác đều cạnh a nên BN = AN
Do đó tam giác ABN cân tại N mà M là trung điểm AB
\( \Rightarrow \) \(AB \bot MN\)
Vậy MN là đường vuông góc chung của AB và CD.
b) Ta có \(CD \bot \left( {ABN} \right);AB \subset \left( {ABN} \right) \Rightarrow CD \bot AB\)
Chứng minh tương tự ta được \(BC \bot AD,BD \bot AC\)
Vậy các cặp cạnh đối diện trong tứ diện ABCD đều vuông góc với nhau
