
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AA’ = a, AB = b, BC = c.
a) Tính khoảng cách giữa CC’ và (BB’D’D).
b) Xác định đường vuông góc chung và tính khoảng cách giữa AC và B’D’.

- Khoảng cách giữa đường thẳng a và mặt phẳng (P) song song với a là khoảng cách từ một điểm bất kì trên a đến (P).
- Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa hai mặt phẳng song song, tương ứng chứa hai đường thẳng đó.

Advertisements (Quảng cáo)
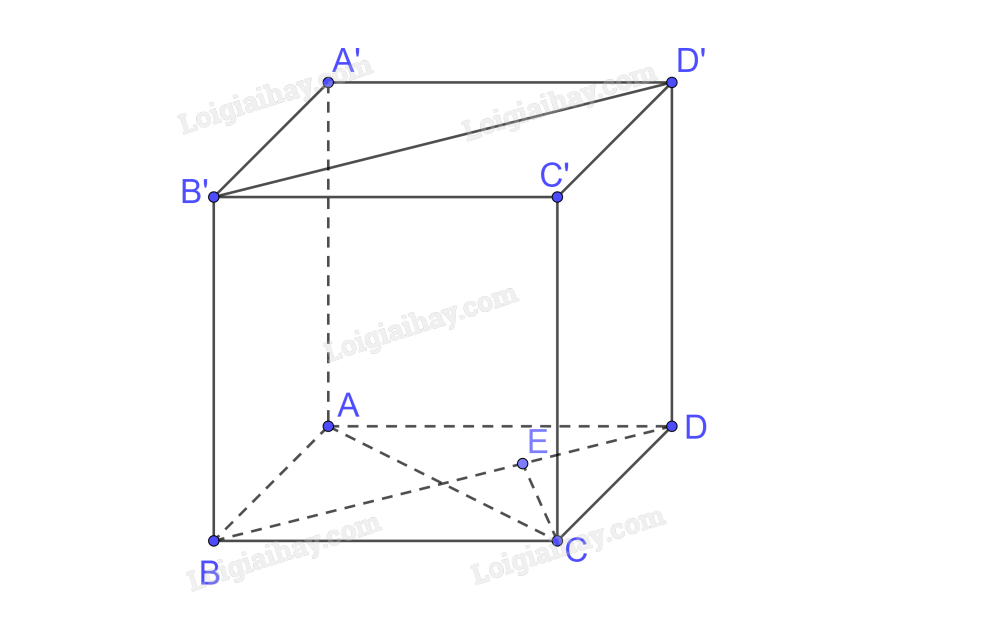
a) Trong (ABCD) kẻ \(CE \bot BD\)
Mà \(CE \bot BB’\left( {BB’ \bot \left( {ABCD} \right)} \right) \Rightarrow CE \bot \left( {BB’D’D} \right)\)
Ta có CC’ // BB’ \( \Rightarrow \) CC’ // (BB’D’D) \( \Rightarrow \) d(CC’, (BB’D’D)) = d(C, (BB’D’D)) = CE
Xét tam giác BCD vuông tại C có
\(\frac{1}{{C{E^2}}} = \frac{1}{{B{C^2}}} + \frac{1}{{C{D^2}}} = \frac{1}{{{c^2}}} + \frac{1}{{{b^2}}} = \frac{{{b^2} + {c^2}}}{{{c^2}{b^2}}} \Rightarrow CE = \frac{{bc}}{{\sqrt {{b^2} + {c^2}} }}\)
b) \(AC \subset \left( {ABCD} \right),B’D’ \subset \left( {A’B’C’D’} \right),\left( {ABCD} \right)//\left( {A’B’C’D’} \right)\)
\( \Rightarrow d\left( {AC,B’D’} \right) = d\left( {\left( {ABCD} \right),\left( {A’B’C’D’} \right)} \right) = BB’ = a\)
