
Cho khối chóp đều S.ABC, đáy có cạnh bằng a, cạnh bên bằng b. Tính thể tích của khối chóp đó. Từ đó suy ra thể tích của khối tứ diện đều có cạnh bằng a.

Thế tích khối chóp \(V = \frac{1}{3}h.S\)

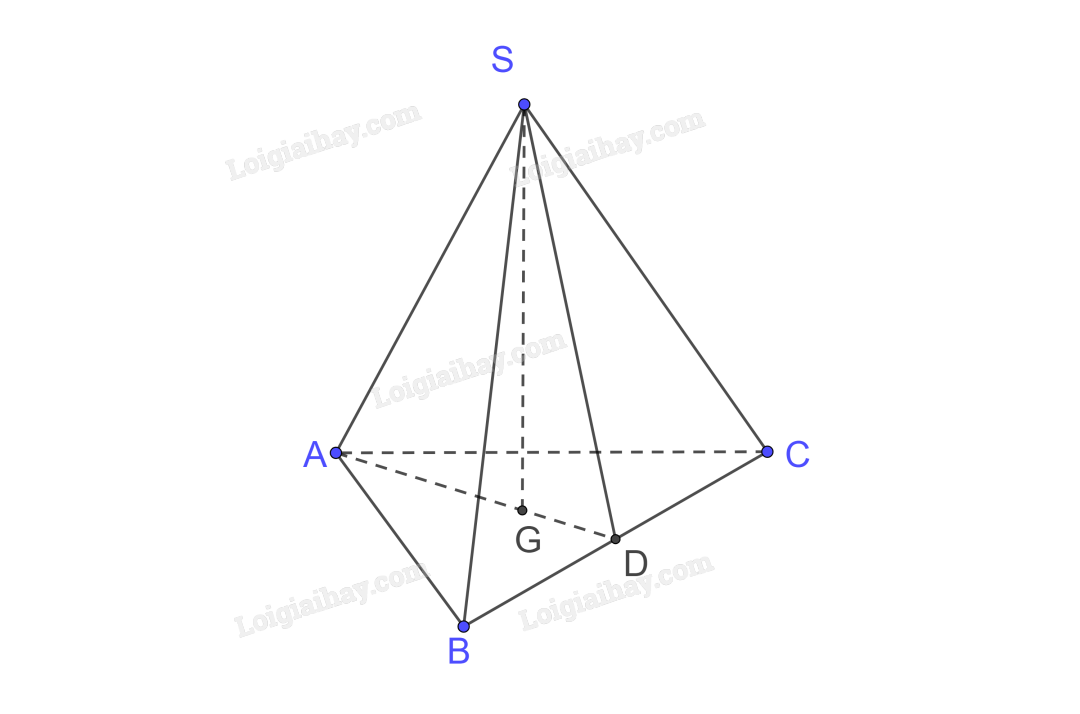
Vì hình chóp S.ABC đều, gọi G là hình chiếu của S trên (ABC) nên G là tâm của đáy ABC là tam giác đều do đó G cũng là trọng tâm hay trực tâm của tam giác ABC.
Gọi AG cắt BC tại D
Advertisements (Quảng cáo)
Tam giác ABC đều cạnh a nên \(AD = \frac{{a\sqrt 3 }}{2}\)
Mà G là trọng tâm nên \(AG = \frac{2}{3}AD = \frac{{a\sqrt 3 }}{3}\)
Xét tam giác SAG vuông tại G có
\(SG = \sqrt {S{A^2} - A{G^2}} = \sqrt {{b^2} - {{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}} = \sqrt {{b^2} - \frac{{{a^2}}}{3}} \)
Diện tích tam giác đều ABC là ${{S}_{\vartriangle ABC}}=\frac{{{a}^{2}}\sqrt{3}}{4}$
Thể tích khối chóp đều là $V=\frac{1}{3}SG.{{S}_{\vartriangle ABC}}=\frac{1}{3}.\sqrt{{{b}^{2}}-\frac{{{a}^{2}}}{3}}.\frac{{{a}^{2}}\sqrt{3}}{4}=\frac{{{a}^{2}}\sqrt{3}}{12}.\sqrt{{{b}^{2}}-\frac{{{a}^{2}}}{3}}$
Do đó thể tích của khối tứ diện đều có cạnh bằng a là
\(V = \frac{{{a^2}\sqrt 3 }}{{12}}.\sqrt {{a^2} - \frac{{{a^2}}}{3}} = \frac{{{a^3}\sqrt 2 }}{{12}}\)
