Giải câu hỏi trang 61, 62, 63 Toán 11 tập 2 - Kết nối tri thức: Khi mua máy điều hoà...

Hoạt động 1

Khi mua máy điều hoà, bác An được hướng dẫn rằng mỗi mét khối của phòng cần công suất điều hoà khoảng 200 BTU. Căn phòng bác An cần lắp máy có dạng hình hộp chữ nhật, rộng 4 m, dài 5 m và cao 3 m. Hỏi bác An cần mua loại điều hoà có công suất bao nhiêu BTU?

Thể tích hình hộp chữ nhật = chiều dài x chiều rộng x chiều cao

Thể tích của căn phòng là:

$V = 4.5.3 = 60\left( {{m^3}} \right)$

Vì mỗi mét khối của phòng cần công suất điều hoà khoảng 200 BTU nên công suất cần thiết cho máy điều hoà của căn phòng bác An là:

60.200 = 12000 BTU

Do đó, bác An cần mua một máy điều hoà có công suất khoảng 12 000 BTU để làm mát cho căn phòng của mình.

Luyện tập 1

Cho khối chóp đều S.ABCD có cạnh đáy bằng a, cạnh bên bằng b. Tính thể tích của khối chóp.

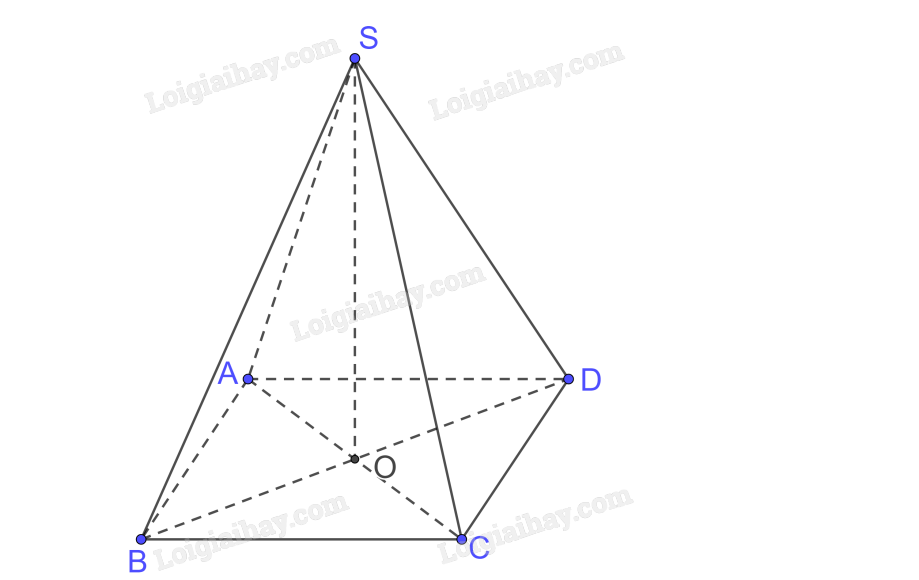
Thế tích khối chóp $V = \frac{1}{3}h.S$

Gọi $AC \cap BD = \left\{ O \right\}$ mà S.ABCD đều nên $SO \bot \left( {ABCD} \right)$

Xét tam giác ABC vuông tại B có $AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2$

$\Rightarrow OA = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2}$

Xét tam giác SAO vuông tại O có

$SO = \sqrt {S{A^2} - A{O^2}} = \sqrt {{b^2} - {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}} = \sqrt {{b^2} - \frac{{{a^2}}}{2}} = \frac{{\sqrt {4{b^2} - 2{a^2}} }}{2}$

${S_{ABCD}} = {a^2}$

Vậy khối chóp có thể tích $V = \frac{1}{3}SO.{S_{ABCD}} = \frac{1}{3}.\frac{{\sqrt {4{b^2} - 2{a^2}} }}{2}.{a^2} = \frac{{{a^2}\sqrt {4{b^2} - 2{a^2}} }}{6}$

Luyện tập 2

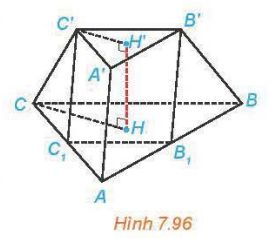
Cho khối chóp cụt đều ABC.A’B’C’ có đường cao HH’ = h, hai mặt đáy ABC, A’B’C’ có cạnh tương ứng bằng 2a, a.

a) Tính thể tích của khối chóp cụt.

b) Gọi B₁,C₁ tương ứng là trung điểm của AB, AC. Chứng minh rằng AB₁C₁.A’B’C’ là một hình lăng trụ. Tính thể tích khối lăng trụ AB₁C₁.A’B’C’.

Thể tích khối chóp cụt đều $V = \frac{1}{3}.h.\left( {S + S’ + \sqrt {S.S’} } \right)$

Thể tích khối lăng trụ $V = h.S$

a) Tam giác đều ABC có diện tích $S = \frac{{{{\left( {2a} \right)}^2}\sqrt 3 }}{4} = {a^2}\sqrt 3$

Tam giác đều A’B’C’ có diện tích $S’ = \frac{{{a^2}\sqrt 3 }}{4}$

Thể tích khối chóp cụt

$V = \frac{1}{3}.HH’.\left( {S + S’ + \sqrt {S.S’} } \right) = \frac{1}{3}.h.\left( {{a^2}\sqrt 3 + \frac{{{a^2}\sqrt 3 }}{4} + \sqrt {{a^2}\sqrt 3 .\frac{{{a^2}\sqrt 3 }}{4}} } \right) = \frac{{7{a^2}\sqrt 3 }}{{12}}$

b) Vì ABC.A’B’C’ là khối chóp cụt đều nên (ABC) // (A’B’C’)

Mà $\left( {A{B_1}{C_1}} \right) \subset \left( {ABC} \right) \Rightarrow \left( {A{B_1}{C_1}} \right)//\left( {A’B’C’} \right)$

Xét tam giác ABC có

B₁,C₁ tương ứng là trung điểm của AB, AC

$\Rightarrow$ B₁C₁ là đường trung bình của tam giác ABC

$\Rightarrow$ ${B_1}{C_1} = \frac{{BC}}{2}$ và B₁C₁ // BC mà $B’C’ = \frac{{BC}}{2}$ và BC // B’C’

$\Rightarrow$ B₁C₁ = B’C’ và B₁C₁ // B’C’ $\Rightarrow$ C₁C’B’B₁ là hình bình hành

Ta có $A{B_1} = A’B’ = \frac{{AB}}{2},A{B_1}//A’B’$ $\Rightarrow$ AA’B’B₁ là hình bình hành.

$A{C_1} = A’C’ = \frac{{AC}}{2},A{C_1}//A’C’$ $\Rightarrow$ AA’C’C₁ là hình bình hành.

Do đó AB₁C₁.A’B’C’ là một hình lăng trụ

Thể tích hình lăng trụ $V = HH’.S’ = h.\frac{{{a^2}\sqrt 3 }}{4}$

Vận dụng

Một sọt đựng đồ có dạng hình chóp cụt đều (H.7.98). Đáy và miệng sọt là các hình vuông tương ứng có cạnh bằng 30 cm, 60 cm, cạnh bên của sọt dài 50 cm. Tính thể tích của sọt.

Thể tích khối chóp cụt đều $V = \frac{1}{3}.h.\left( {S + S’ + \sqrt {S.S’} } \right)$

Diện tích mặt đáy lớn là ${S_1} = {60^2}\left( {c{m^2}} \right)$

Diện tích mặt đáy nhỏ là ${S_2} = {30^2}\left( {c{m^2}} \right)$

Chiều cao là $h = \sqrt {{{50}^2} - \frac{{{{30}^2}}}{2}} = 5\sqrt {82} \left( {cm} \right)$

$V = \frac{1}{3}h\left( {{S_1} + {S_2} + \sqrt {{S_1}{S_2}} } \right) \approx 95082\left( {c{m^3}} \right)$