
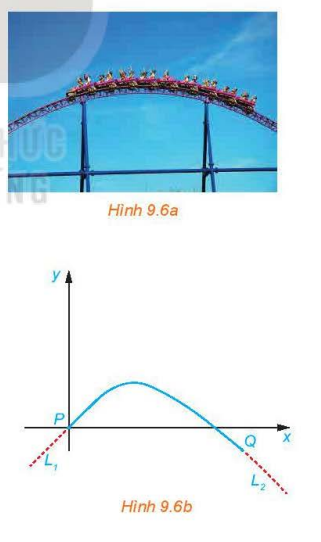
Một kĩ sư thiết kế một đường ray tàu lượn, mà mặt cắt của nó gồm một cung đường cong có dạng parabol (H.9.6a), đoạn dốc lên \({L_1}\) và đoạn dốc xuống \({L_2}\) là những phần đường thẳng có hệ số góc lần lượt là 0,5 và –0,75. Để tàu lượn chạy êm và không bị đổi hướng đột ngột, \({L_1}\) và \({L_2}\) phải là những tiếp tuyến của cung parabol tại các điểm chuyển tiếp P và Q (H.9.6b). Giả sử gốc toạ độ đặt tại P và phương trình của parabol là \(y = a{x^2} + bx + c,\) trong đó x tính bằng mét.
a) Tìm c.
b) Tính y'(0) và tìm b.
c) Giả sử khoảng cách theo phương ngang giữa P và Q là 40 m. Tìm a.
d) Tìm chênh lệch độ cao giữa hai điểm chuyển tiếp P và Q.

Hệ số góc của tiếp tuyến là \(f’\left( {{x_0}} \right)\)
Advertisements (Quảng cáo)

a) Vì gốc toạ độ đặt tại P nên P(0;0) do đó ta có c = y(0) = 0
b) \(y’ = 2ax + b \Rightarrow y’\left( 0 \right) = b\)
Mà L1 là phương trình tiếp tuyến tại P có hệ số góc 0,5 nên \(y’\left( 0 \right) = 0,5 \Rightarrow b = 0,5\)
c) L2 là phương trình tiếp tuyến tại Q có hệ số góc – 0,75 nên \(y’\left( {{x_Q}} \right) = 2a{x_Q} + 0,5 = - 0,75\)
Vì khoảng cách theo phương ngang giữa P và Q là 40 m nên \({x_Q} - {x_P} = {x_Q} = 40\)
\( \Rightarrow 2a.40 + 0,5 = - 0,75 \Rightarrow a = \frac{{ - 1}}{{64}}\)
d) \({y_Q} = \frac{{ - 1}}{{64}}{.40^2} + 0,5.40 = - 5\)
Vậy chênh lệch độ cao giữa hai điểm chuyển tiếp P và Q là \(\left| {{y_P} - {y_Q}} \right| = 5\)
