Giải mục 1 trang 54, 55 Toán 11 tập 2 - Kết nối tri thức: Tam giác ABC’ là tam giác gì? Tính khoảng cách từ A đến BC’...

Hoạt động 1

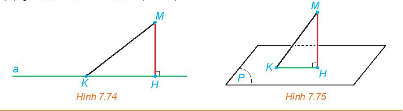
a) Cho điểm M và đường thẳng a. Gọi H là hình chiếu của M trên a. Với mỗi điểm K thuộc a, vì sao MK ≥ MH (H.7.74)

b) Cho điểm M và mặt phẳng (P). Gọi H là hình chiếu của M trên (P). Với mỗi điểm K thuộc (P), giải thích vì sao MK ≥ MH (H.7.75).

Dựa vào mối quan hệ đường xiên và đường vuông góc.

a) Vì H là hình chiếu của M trên đường thẳng a, nên MH là khoảng cách từ M đến a và MH là đoạn thẳng ngắn nhất từ M đến a, suy ra MK ≥ MH.

b) Vì H là hình chiếu của M trên (P) nên MH vuông góc với (P) do đó MH vuông góc với HK.

Dựa vào mối quan hệ đường xiên và đường vuông góc ta có MK ≥ MH.

Luyện tập 1

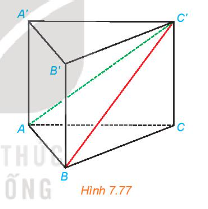
Cho hình lăng trụ đứng ABC.A’B’C’ có ABC là tam giác vuông cân tại A, AB = a, AA’ = h (H.7.77).

a) Tính khoảng cách từ A đến mặt phẳng (BCC’B’).

b) Tam giác ABC’ là tam giác gì? Tính khoảng cách từ A đến BC’.

- Khoảng cách từ một điểm M đến một đường thẳng a, kí hiệu d (M, a), là khoảng cách giữa M và hình chiếu H của M trên a.

- Khoảng cách từ một điểm M đến một mặt phẳng (P), kí hiệu d (M, (P)), là khoảng cách giữa M và hình chiếu H của M trên (P).

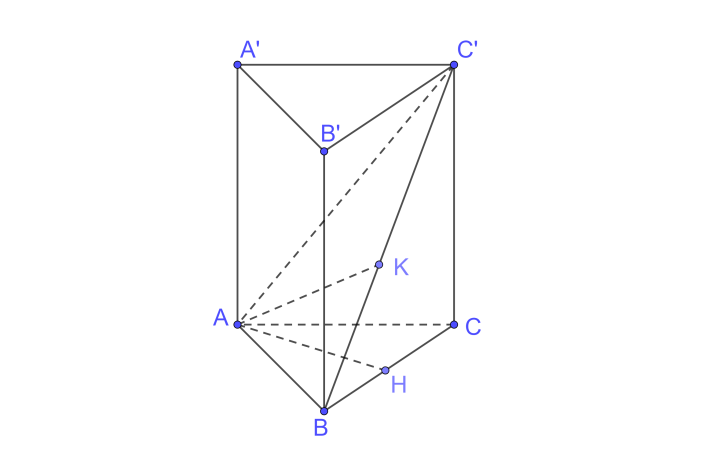
a) Ta có $BB’ \bot \left( {ABC} \right);BB’ \subset \left( {BCC’B’} \right) \Rightarrow \left( {ABC} \right) \bot \left( {BCC’B’} \right)$

$\left( {ABC} \right) \cap \left( {BCC’B’} \right) = BC$

(ABC): Kẻ $AH \bot BC$

$\Rightarrow AH \bot \left( {BCC’B’} \right) \Rightarrow d\left( {A,\left( {BCC’B’} \right)} \right) = AH$

Xét tam giác ABC vuông cân tại A có

$\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{2}{{{a^2}}}$ (hệ thức lượng trong tam giác vuông)

$\Rightarrow AH = \frac{{a\sqrt 2 }}{2}$

b) +) Ta có $AB \bot AC,AB \bot AA’\left( {AA’ \bot \left( {ABC} \right)} \right) \Rightarrow AB \bot \left( {ACC’A’} \right);AC’ \subset \left( {ACC’A’} \right) \Rightarrow AC’ \bot AB$

Do đó tam giác ABC’ là tam giác vuông.

+) Trên (ABC’) kẻ $AK \bot BC’ \Rightarrow d\left( {A,BC’} \right) = AK$

Xét tam giác ACC’ vuông tại C có

$A{C’^2} = A{C^2} + C{C’^2} = {a^2} + {h^2}$ (Định lí Pytago)

Xét tam giác ABC’ vuông tại A có

$\begin{array}{l}\frac{1}{{A{K^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{{C’}^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{a^2} + {h^2}}} = \frac{{2{a^2} + {h^2}}}{{{a^2}\left( {{a^2} + {h^2}} \right)}} \Rightarrow A{K^2} = \frac{{{a^2}\left( {{a^2} + {h^2}} \right)}}{{2{a^2} + {h^2}}}\\ \Rightarrow AK = a.\sqrt {\frac{{{a^2} + {h^2}}}{{2{a^2} + {h^2}}}} \end{array}$