Hoạt động 2
Cho hai hàm số \(f\left( x \right) = {x^2}\) và \(g\left( x \right) = {x^3}\), với các đồ thị như hình dưới đây.
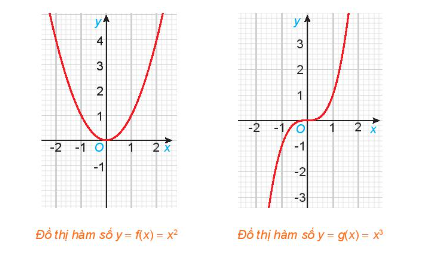
a) Tìm các tập xác định \({D_f},\;{D_g}\) của các hàm số \(f\left( x \right)\) và \(g\left( x \right)\).
b) Chứng tỏ rằng \(f\left( { - x} \right) = f\left( x \right),\;\forall x \in {D_f}\). Có nhận xét gì về tính đối xứng của đồ thị hàm số \(y = f\left( x \right)\) đối với hệ trục tọa độ Oxy?
c) Chứng tỏ rằng \(g\left( { - x} \right) = - g\left( x \right),\;\forall x \in {D_g}\). Có nhận xét gì về tính đối xứng của đồ thị hàm số \(y = g\left( x \right)\) đối với hệ trục tọa độ Oxy?

Hàm số \(f\left( x \right)\) và \(g\left( x \right)\) luôn xác định với mọi \(x \in \mathbb{R}\)

a) Tập xác định của hàm số đã cho là: \({D_f} = \mathbb{R};\;{D_g} = \mathbb{R}\)
b) Ta có: \(f\left( { - x} \right) = {\left( { - x} \right)^2} = {x^2} = f\left( x \right)\)
Đồ thị của hàm số \(y = f\left( x \right) = {x^2}\) đối xứng qua trục tung
c) Ta có: \(g\left( { - x} \right) = {\left( { - x} \right)^3} = - {x^3} = - g\left( x \right)\)
Đồ thị của hàm số \(y = g\left( x \right) = {x^3}\) đối xứng qua gốc tọa độ
Luyện tập
Xét tính chẵn, lẻ của hàm số \(g\left( x \right) = \frac{1}{x}\).

Sử dụng định nghĩa về hàm số chẵn, lẻ

Tập xác định của hàm số là \(D = \mathbb{R}\;\backslash \left\{ 0 \right\}\)
Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D
Ta có: \(g\left( { - x} \right) = \frac{1}{{ - x}} = - \frac{1}{x} = - g\left( x \right),\;\forall x\; \in \;D\).
Advertisements (Quảng cáo)
Vậy \(g\left( x \right) = \frac{1}{x}\) là hàm số lẻ
Hoạt động 3
So sánh:
a) \(\sin \left( {x + 2\pi } \right)\) và \(\sin x\);
b) \(\cos (x + 2\pi )\) và \(\cos x\);
c) \(\tan \left( {x + \pi } \right)\) và \(\tan x\);
d) \(\cot (x + \pi )\) và \(\cot x\).

Ta có:
a) \(\sin \left( {x + 2\pi } \right) = \sin x\) với mọi \(x\; \in \;\mathbb{R}\)
b) \(\cos \left( {x + 2\pi } \right) = \cos x\) với mọi \(x\; \in \;\mathbb{R}\)
c) \(\tan \left( {x + \pi } \right) = \tan x\) với mọi \(x \ne \frac{\pi }{2} + k\pi ,\;k\; \in \;\mathbb{Z}\)
d) \(\cot \left( {x + \pi } \right) = \cot x\) với mọi \(x \ne \frac{\pi }{2} + k\pi ,\;k\; \in \;\mathbb{Z}\)
Luyện tập 3
Xét tính tuần hoàn của hàm số \(y = \tan 2x\).

Hàm số \(y = \tan \left( {ax + b} \right)\) tuần hoàn với chu kỳ \(T = \frac{\pi }{{\left| a \right|}}\)

Hàm số có tập xác định là \(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,\;k\; \in \;\mathbb{Z}} \right\}\) và với mọi số thực x, ta có:
\(\left( {x - \frac{\pi }{2}} \right) \in \;\mathbb{R},\;\left( {x + \frac{\pi }{2}} \right) \in \;\mathbb{R},\)
\(\tan 2\left( {x + \frac{\pi }{2}} \right) = \tan \left( {2x + \pi } \right) = \tan 2x\)
Vậy \(y = \tan 2x\;\)là hàm số tuần hoàn
