Hoạt động2
Đối với hai cánh cửa trong Hình 7.5, tính góc giữa hai đường mép cửa BC và MN


Để xác định góc giữa hai đường thẳng chéo nhau a và b, ta có thể lấy một điểm O thuộc đường thẳng a và qua đó kẻ đường thẳng b’ song song với b. Khi đó (a, b) = (a’, b’)

Vì BC // PN nên (BC, MN) = (PN, MN)
Mà PN vuông góc với MN nên góc giữa hai đường mép này bằng 900.
Câu hỏi
Nếu đường thẳng a vuông góc với đường thẳng b thì a có vuông góc với các đường thẳng song song với b hay không?

\(\left. \begin{array}{l}a \bot b\\b//c\end{array} \right\} \Rightarrow a \bot c\)

Nếu đường thẳng a vuông góc với đường thẳng b thì a có vuông góc với các đường thẳng song song với b.
Luyện tập1
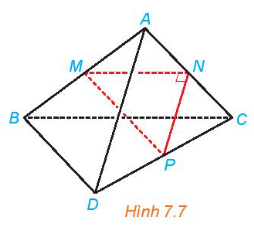
Cho tam giác MNP vuông tại N và một điểm A nằm ngoài mặt phẳng (MNP). Lần lượt lấy các điểm B, C, D sao cho M, N, P tương ứng là trung điểm của AB, AC, CD (H.7.7). Chứng minh rằng AD và BC vuông góc với nhau và chéo nhau.
Advertisements (Quảng cáo)

Nếu đường thẳng a vuông góc với đường thẳng b thì a có vuông góc với các đường thẳng song song với b.

+) Xét tam giác ABC có
M, N lần lượt là trung điểm của AB, AC
\( \Rightarrow \) MN là đường trung bình của tam giác ABC
\( \Rightarrow \) MN // BC
Mà NP \( \bot \) MN nên NP \( \bot \) BC
Xét tam giác ADC có
N, P lần lượt là trung điểm của AC, CD
\( \Rightarrow \) PN là đường trung bình của tam giác ADC
\( \Rightarrow \) PN // AD
Mà NP \( \bot \) BC nên AD \( \bot \) BC
+) BC // MN mà \(MN \subset \left( {MNP} \right) \Rightarrow BC//\left( {MNP} \right)\)
PN // AD mà \(PN \subset \left( {MNP} \right) \Rightarrow AD//\left( {MNP} \right)\)
Vậy AD và BC chéo nhau.
