Hoạt động 3
Một máy bay giữ vận tốc không đổi, với độ lớn 240km/h trong suốt 2 phút đầu kể từ khi cất cánh. Hỏi thông tin trên có đủ để ta xác định độ cao của máy bay so với mặt đất phẳng, tại thời điểm 1 phút kể từ khi máy bay cất cánh không?


Quãng đường = vận tốc x thời gian

Thông tin trên không đủ để ta xác định độ cao của máy bay so với mặt đất phẳng, tại thời điểm 1 phút kể từ khi máy bay cất cánh mà chỉ tính được quãng đường bay của máy bay bay được.
Vận dụng
Tâm Trái Đất chuyển động quanh Mặt Trời theo quỹ đạo là một đường elip nhận tâm Mặt Trời làm tiêu điểm. Trong quá trình chuyển động, Trái Đất lại quay quanh trục Bắc Nam. Trục này có phương không đổi và luôn tạo với mặt phẳng chứa quỹ đạo một góc khoảng 66,5°.
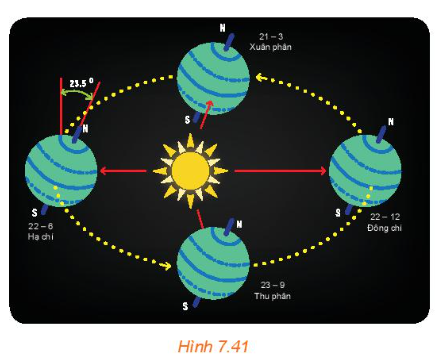
(Theo nationalgeographic.org).
a) Giải thích vì sao hình chiếu của trục Trái Đất trên mặt phẳng quỹ đạo (P) cũng có phương không đổi.
b) Giải thích vì sao có hai thời điểm trong năm mà tại đó hình chiếu của trục Trái Đất trên mặt phẳng (P) thuộc đường thẳng nối tâm Mặt Trời và tâm Trái Đất.

Quan sát hình kết hợp xác định hình chiếu

a) Vì trục quay của Trái Đất luôn cố định hướng về một phương cố định trong không gian, và mặt phẳng quỹ đạo cũng không thay đổi trong quá trình quay quanh Mặt Trời.
b) Trong quá trình chuyển động quanh Mặt Trời, hình chiếu của trục Trái Đất trên mặt phẳng quỹ đạo sẽ thay đổi theo thời gian và tạo thành một đường tròn có bán kính bằng góc nghiêng của trục quay so với mặt phẳng quỹ đạo. Khi Trái Đất ở vị trí xa nhất (khoảng 4/7 quỹ đạo) và gần nhất (khoảng 3/7 quỹ đạo) so với Mặt Trời, thì hình chiếu của trục quay của Trái Đất trên mặt phẳng quỹ đạo sẽ nằm trên đường thẳng nối tâm Trái Đất và Mặt Trời.
Khám phá
Advertisements (Quảng cáo)
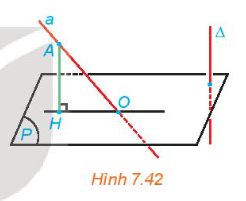
Cho đường thẳng \(\Delta \) vuông góc với mặt phẳng (P). Khi đó, với một đường thẳng a bất kì, góc giữa a và (P) có mối quan hệ gì với góc giữa a và \(\Delta \)?

- Nếu b // b’ thì (a, b) = (a, b’)
- Góc giữa đường thẳng a với mặt phẳng (P) là góc giữa a và hình chiếu a’ của nó trên (P).

+) AH // \(\Delta \) (cùng vuông góc (P))
\( \Rightarrow \) (a, \(\Delta \)) = (a, AH) = \(\widehat {HAO}\)
+) HO là hình chiếu của a trên (P)
\( \Rightarrow \) (a, (P)) = (a, HO) = \(\widehat {AOH}\)
Mà tam giác AHO vuông tại H \( \Rightarrow \) \(\widehat {HAO}\) và \(\widehat {AOH}\) phụ nhau.
\( \Rightarrow \) Góc giữa a và (P) có mối quan hệ với góc giữa a và \(\Delta \) là 2 góc phụ nhau.
TN
Đo góc giữa một sợi dây kéo căng và mặt bàn hoặc sàn lớp học. (Có thể cho một đầu sợi dây huộc mặt bàn, mặt sàn để thuận tiện hơn cho việc đo.)

Thực hành sử dụng thước đo góc.

Để đo góc giữa một sợi dây kéo căng và mặt bàn hoặc sàn lớp học, ta có thể sử dụng thước góc và thực hiện các bước sau:
