Hoạt động 4
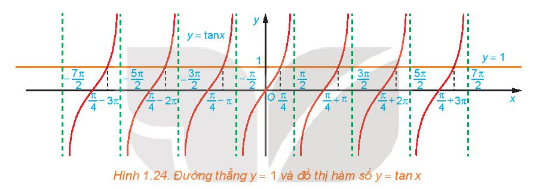
a) Quan sát Hình 1.24, hãy cho biết đường thẳng \(y = 1\) cắt đồ thị hàm số \(y = \tan x\) tại mấy điểm trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)?\)
b) Dựa vào tính tuần hoàn của hàm tang, hãy viết công thức nghiệm của phương trình đã cho

Nghiệm của phương trình \(\tan x = 1\) là hoành độ các giao điểm của đường thẳng \(y = 1\) và đồ thị hàm số \(y = \tan x\)

a) Từ Hình 1.24, ta thấy đường thẳng \(y = 1\) cắt đồ thị hàm số \(y = \tan x\;\)tại 1 điểm \(x = \frac{\pi }{4}\) trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\)
b) Ta có công thức nghiệm của phương trình là: \(x = \frac{\pi }{4} + k\pi \;\left( {k \in \mathbb{Z}} \right)\)
Advertisements (Quảng cáo)
Luyện tập 4
Giải các phương trình sau:
a) \(\sqrt 3 \tan 2x = - 1\); b) \(\tan 3x + \tan 5x = 0\)’

Dựa vào công thức nghiệm tổng quát: \(\tan x = m\; \Leftrightarrow \tan x = \tan \alpha \Leftrightarrow x = \alpha + k\pi \;\left( {k \in \mathbb{Z}} \right)\)

a) \(\sqrt 3 \tan 2x = - 1\;\; \Leftrightarrow \tan 2x = - \frac{1}{{\sqrt 3 }}\;\;\; \Leftrightarrow \tan 2x = \tan - \frac{\pi }{6}\; \Leftrightarrow 2x = - \frac{\pi }{6} + k\pi \)
\(\;\; \Leftrightarrow x = - \frac{\pi }{{12}} + \frac{{k\pi }}{2}\;\left( {k \in \mathbb{Z}} \right)\)
b) \(\tan 3x + \tan 5x = 0\;\; \Leftrightarrow \tan 3x = \tan \left( { - 5x} \right) \Leftrightarrow 3x = - 5x + k\pi \;\; \Leftrightarrow 8x = k\pi \;\; \Leftrightarrow x = \frac{{k\pi }}{8}\;\left( {k \in \mathbb{Z}} \right)\)
