Lý thuyết Công thức lượng giác - Toán 11 Kết nối tri thức: Công thức cộng \(\begin{array}{l}\sin \left( {a + b} \right) = \sin a\cos b + \cos asinb\\sin\left( {a - b} \right)...

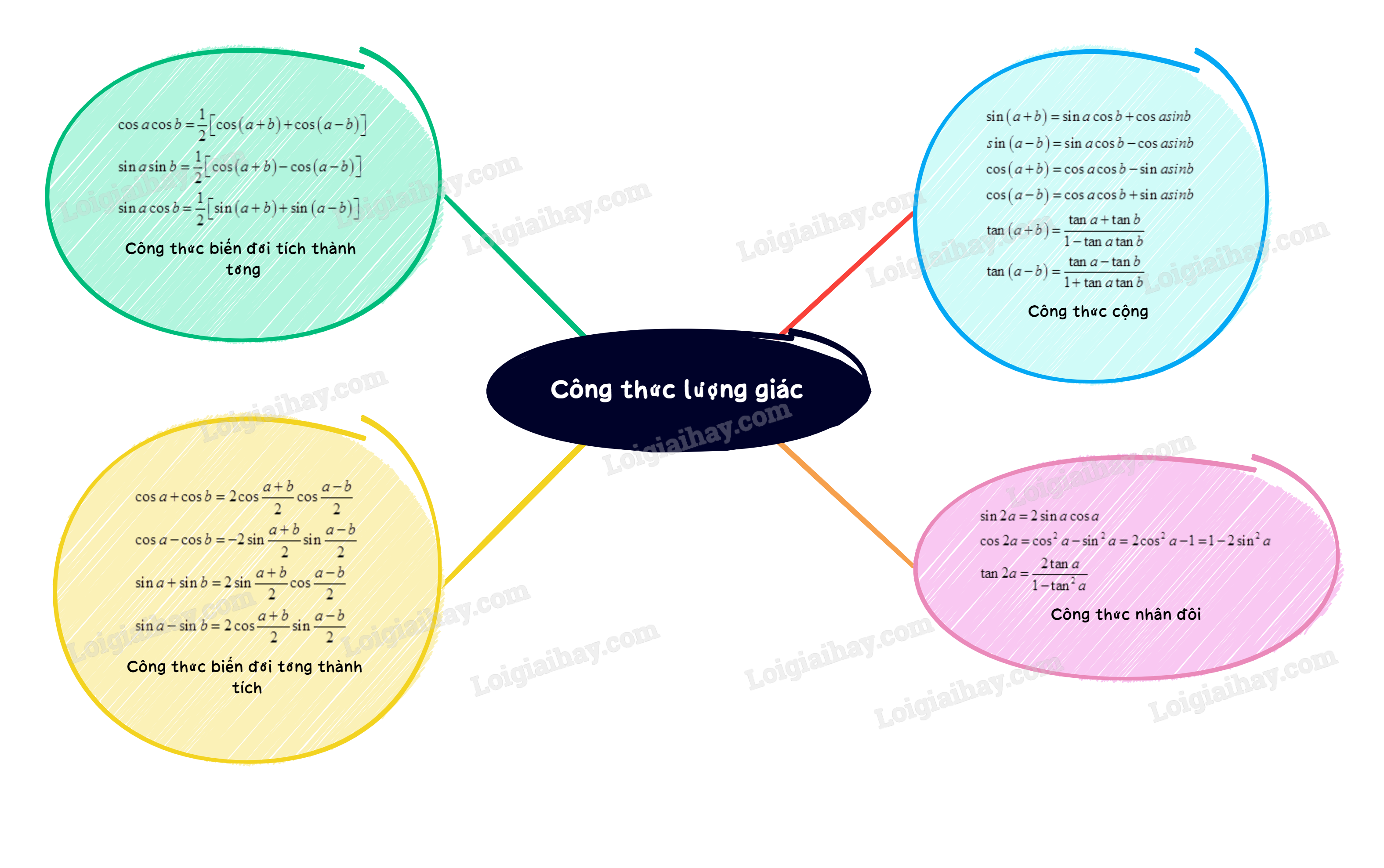
1. Công thức cộng

$\begin{array}{l}\sin \left( {a + b} \right) = \sin a\cos b + \cos asinb\\sin\left( {a - b} \right) = \sin a\cos b - \cos asinb\\\cos \left( {a + b} \right) = \cos a\cos b - \sin asinb\\\cos \left( {a - b} \right) = \cos a\cos b + \sin asinb\\\tan \left( {a + b} \right) = \frac{{\tan a + \tan b}}{{1 - \tan a\tan b}}\\\tan \left( {a - b} \right) = \frac{{\tan a - \tan b}}{{1 + \tan a\tan b}}\end{array}$

2. Công thức nhân đôi

$\begin{array}{l}\sin 2a = 2\sin a\cos a\\\cos 2a = {\cos ^2}a - {\sin ^2}a = 2{\cos ^2}a - 1 = 1 - 2{\sin ^2}a\\\tan 2a = \frac{{2\tan a}}{{1 - {{\tan }^2}a}}\end{array}$

Suy ra, công thức hạ bậc:

${\sin ^2}a = \frac{{1 - \cos 2a}}{2},{\cos ^2}a = \frac{{1 + \cos 2a}}{2}$

3. Công thức biến đổi tích thành tổng

$\begin{array}{l}\cos a\cos b = \frac{1}{2}\left[ {\cos \left( {a + b} \right) + \cos \left( {a - b} \right)} \right]\\\sin a\sin b = \frac{1}{2}\left[ {\cos \left( {a - b} \right) - \cos \left( {a + b} \right)} \right]\\\sin a\cos b = \frac{1}{2}\left[ {\sin \left( {a + b} \right) + \sin \left( {a - b} \right)} \right]\end{array}$

4. Công thức biến đổi tổng thành tích

$\begin{array}{l}\cos a + \cos b = 2\cos \frac{{a + b}}{2}\cos \frac{{a - b}}{2}\\\cos a - \cos b = - 2\sin \frac{{a + b}}{2}\sin \frac{{a - b}}{2}\\\sin a + \sin b = 2\sin \frac{{a + b}}{2}\cos \frac{{a - b}}{2}\\\sin a - \sin b = 2\cos \frac{{a + b}}{2}\sin \frac{{a - b}}{2}\end{array}$