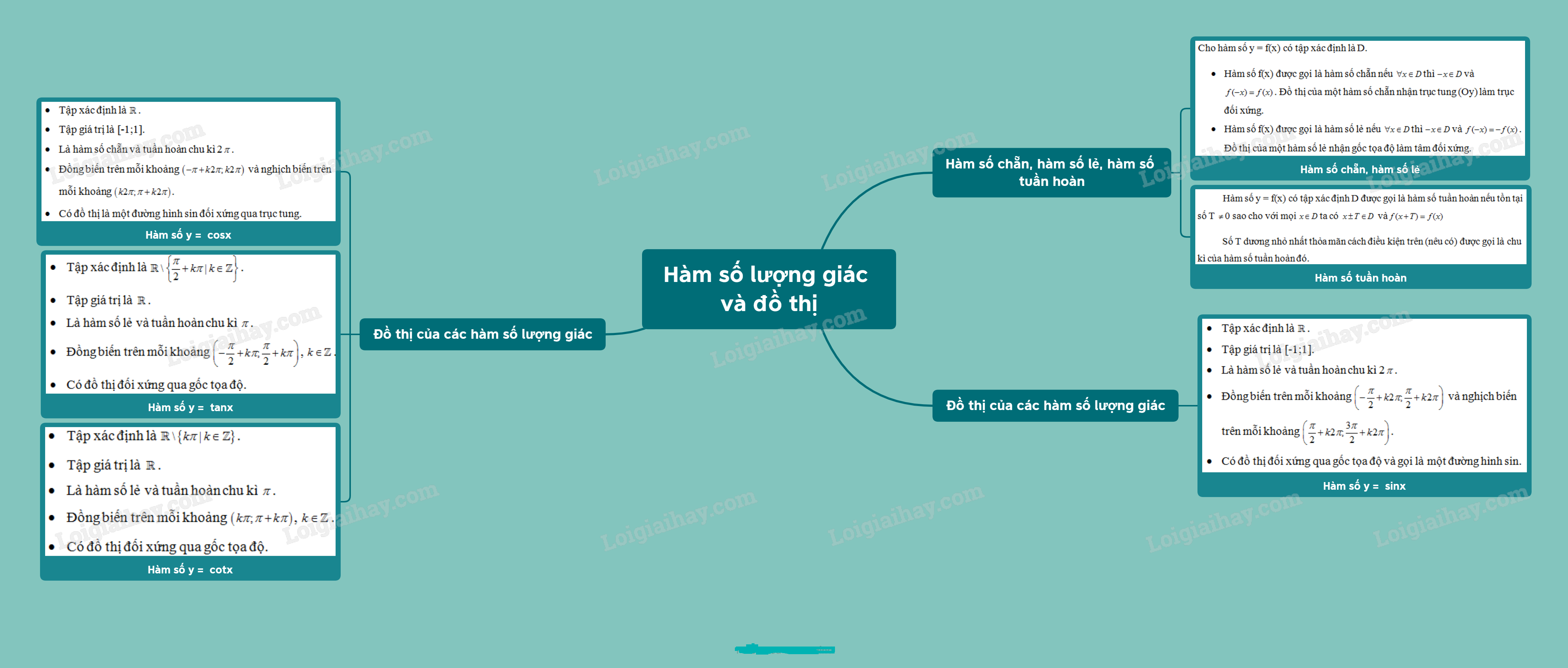
Lý thuyết Hàm số lượng giác - Toán 11 Kết nối tri thức...

1. Định nghĩa hàm số lượng giác

• Quy tắc đặt tương ứng mỗi số thực x với số thực sinx được gọi là hàm số sin, kí hiệu y = sinx. Tập xác định của hàm số sin là $\mathbb{R}$.
• Quy tắc đặt tương ứng mỗi số thực x với số thực cosx được gọi là hàm số cos, kí hiệu y = cosx. Tập xác định của hàm số côsin là $\mathbb{R}$.
• Hàm số cho bằng công thức $y = \frac{{\sin \alpha }}{{\cos \alpha }}$được gọi là hàm số tang, kí hiệu là y = tanx. Tập xác định của hàm số tang là $\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}$.
• Hàm số cho bằng công thức $y = \frac{{\cos \alpha }}{{\sin \alpha }}$được gọi là hàm số côtang, kí hiệu là y = cotx. Tập xác định của hàm số côtang là $\mathbb{R}\backslash \left\{ {k\pi |k \in \mathbb{Z}} \right\}$.

2. Hàm số chẵn, hàm số lẻ, hàm số tuần hoàn

a, Hàm số chẵn, hàm số lẻ

Cho hàm số y = f(x) có tập xác định là D.

• Hàm số f(x) được gọi là hàm số chẵn nếu $\forall x \in D$ thì $- x \in D$ và $f( - x) = f(x)$. Đồ thị của một hàm số chẵn nhận trục tung (Oy) làm trục đối xứng.
• Hàm số f(x) được gọi là hàm số lẻ nếu $\forall x \in D$ thì $- x \in D$ và $f( - x) = - f(x)$. Đồ thị của một hàm số lẻ nhận gốc tọa độ làm tâm đối xứng.

b, Hàm số tuần hoàn

Hàm số y = f(x) có tập xác định D được gọi là hàm số tuần hoàn nếu tồn tại số T $\ne$0 sao cho với mọi $x \in D$ta có:

• $x + T \in D$và $x - T \in D$
• $f(x + T) = f(x)$

Số T dương nhỏ nhất thỏa mãn cách điều kiện trên (nêu có) được gọi là chu kì của hàm số tuần hoàn đó.

* Nhận xét:

Các hàm số y = sinx, y=cosx tuần hoàn chu kì 2$\pi$.

Các hàm số y = tanx, y=cotx tuần hoàn chu kì $\pi$.

3. Đồ thị và tính chất của hàm số y = sinx

• Tập xác định là $\mathbb{R}$.
• Tập giá trị là [-1;1].
• Là hàm số lẻ và tuần hoàn chu kì 2$\pi$.
• Đồng biến trên mỗi khoảng $\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)$ và nghịch biến trên mỗi khoảng $\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right)$.
• Có đồ thị đối xứng qua gốc tọa độ và gọi là một đường hình sin.

4. Đồ thị và tính chất của hàm số y = cosx

• Tập xác định là $\mathbb{R}$.
• Tập giá trị là [-1;1].
• Là hàm số chẵn và tuần hoàn chu kì 2$\pi$.
• Đồng biến trên mỗi khoảng $\left( { - \pi + k2\pi ;k2\pi } \right)$ và nghịch biến trên mỗi khoảng $\left( {k2\pi ;\pi + k2\pi } \right)$.
• Có đồ thị là một đường hình sin đối xứng qua trục tung.

5. Đồ thị và tính chất của hàm số y = tanx

• Tập xác định là $\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}$.
• Tập giá trị là $\mathbb{R}$.
• Là hàm số lẻ và tuần hoàn chu kì $\pi$.
• Đồng biến trên mỗi khoảng $\left( { - \frac{\pi }{2} + k\pi ;\frac{\pi }{2} + k\pi } \right)$, $k \in \mathbb{Z}$.
• Có đồ thị đối xứng qua gốc tọa độ.

6. Đồ thị và tính chất của hàm số y = cotx

• Tập xác định là $\mathbb{R}\backslash \left\{ {k\pi |k \in \mathbb{Z}} \right\}$.
• Tập giá trị là $\mathbb{R}$.
• Là hàm số lẻ và tuần hoàn chu kì $\pi$.
• Đồng biến trên mỗi khoảng $\left( {k\pi ;\pi + k\pi } \right)$, $k \in \mathbb{Z}$.
• Có đồ thị đối xứng qua gốc tọa độ.
•