Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi G và G’ lần lượt là trọng tâm của tam giác ABC và A’B’C’, I là giao điểm của hai đường thẳng AB’ và A’B. Chứng minh rằng các đường thẳng GI và CG’ song song với nhau.

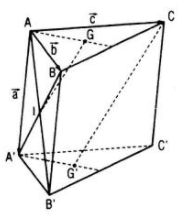
Đặt \(\overrightarrow {AA’} = \overrightarrow a ,\overrightarrow {AB} = \overrightarrow b ,\overrightarrow {AC} = \overrightarrow c \)
Thì \(\overrightarrow {AG} = {1 \over 3}\left( {\overrightarrow b + \overrightarrow c } \right),\overrightarrow {AI} = {1 \over 2}\left( {\overrightarrow a + \overrightarrow b } \right)\)
Advertisements (Quảng cáo)
Do đó, \(\overrightarrow {GI} = \overrightarrow {AI} - \overrightarrow {AG} = {{3\overrightarrow a + \overrightarrow b - 2\overrightarrow c } \over 6}\)
Mặt khác : \(\overrightarrow {AG’} = {1 \over 3}\left( {\overrightarrow {AA’} + \overrightarrow {AB’} + \overrightarrow {AC’} } \right) = \overrightarrow a + {1 \over 3}\left( {\overrightarrow b + \overrightarrow c } \right)\)
\( \Rightarrow \overrightarrow {CG’} = \overrightarrow {AG’} - \overrightarrow {AC} = \overrightarrow a + {1 \over 3}\left( {\overrightarrow b + \overrightarrow c } \right) - \overrightarrow c \)
\(= {{3\overrightarrow a + \overrightarrow b - 2\overrightarrow c } \over 3}\)
Vậy \(\overrightarrow {CG’} = 2\overrightarrow {GI} .\) Ngoài ra, điểm G không thuộc đường thẳng CG’ nên GI và CG’ là hai đường thẳng song song.
