Cho tứ diện ABCD. Lấy các điểm M, N, P. Q lần lượt thuộc AB, BC, CD, DA sao cho
\(\overrightarrow {AM} = {1 \over 3}\overrightarrow {AB} ,\overrightarrow {BN} = {2 \over 3}\overrightarrow {BC},\)
\(\overrightarrow {AQ} = {1 \over 2}\overrightarrow {A{\rm{D}}} ,\overrightarrow {DP} = k\overrightarrow {DC}. \)
Hãy xác định k để bốn điểm P, Q, M, N cùng nằm trên một mặt phẳng.

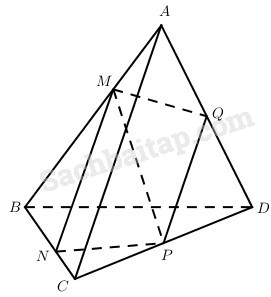
Cách 1
Từ \(\overrightarrow {AM} = {1 \over 3}\overrightarrow {AB} \) ta có \(\overrightarrow {BM} = {2 \over 3}\overrightarrow {BA} \) , mặt khác \(\overrightarrow {BN} = {2 \over 3}\overrightarrow {BC} \) nên MN // AC.
Nếu có k để các điểm M, N, P, Q thuộc một mặt phẳng thì mp(MNQ) cắt mp(ACD) theo giao tuyến PQ nên PQ // AC.
Mặt khác \(\overrightarrow {AQ} = {1 \over 2}\overrightarrow {A{\rm{D}}} \) nên \(\overrightarrow {DP} = {1 \over 2}\overrightarrow {DC} \).
Vậy \(k = {1 \over 2}\) thì các điểm M, N, P, Q cùng thuộc một mặt phẳng.
Cách 2:
Đặt \(\overrightarrow {DA} = \overrightarrow a ,\overrightarrow {DB} = \overrightarrow b ,\overrightarrow {DC} = \overrightarrow c \) .
Khi đó \(\overrightarrow {BC} = \overrightarrow c - \overrightarrow b ,\overrightarrow {AB} = \overrightarrow b - \overrightarrow a \).
Do \(\overrightarrow {AM} = {1 \over 3}\overrightarrow {AB} \)
Advertisements (Quảng cáo)
nên
$$\eqalign{
& \overrightarrow {AM} = {1 \over 3}\left( {\overrightarrow b - \overrightarrow a } \right) = - {1 \over 3}\overrightarrow a + {1 \over 3}\overrightarrow b \cr
& \overrightarrow {AN} = \overrightarrow {AB} + \overrightarrow {BN} = \overrightarrow b - \overrightarrow a + {2 \over 3}\left( {\overrightarrow c - \overrightarrow b } \right) \cr
& = - \overrightarrow a + {1 \over 3}\overrightarrow b + {2 \over 3}\overrightarrow c \cr
& \overrightarrow {AP} = \overrightarrow {A{\rm{D}}} + \overrightarrow {DP} = - \overrightarrow a + k\overrightarrow {DC} = - \overrightarrow a + k\overrightarrow c \cr
& \overrightarrow {AQ} = - {1 \over 2}\overrightarrow a \cr} $$
Khi đó
\(\eqalign{ & \overrightarrow {MN} = - {2 \over 3}\overrightarrow a + {2 \over 3}\overrightarrow c \cr & \overrightarrow {MP} = - {2 \over 3}\overrightarrow a - {1 \over 3}\overrightarrow b + k\overrightarrow c \cr & \overrightarrow {MQ} = - {1 \over 6}\overrightarrow a - {1 \over 3}\overrightarrow b \cr} \)
Các điểm M, N, P, Q thuộc một mặt phẳng khi và chỉ khi có số x, y sao cho
\(\eqalign{& \overrightarrow {MP} = x\overrightarrow {MN} + y\overrightarrow {MQ} \cr & \Leftrightarrow - {2 \over 3}\overrightarrow a - {1 \over 3}\overrightarrow b + k\overrightarrow c \cr & = - {2 \over 3}x\overrightarrow a + {2 \over 3}x\overrightarrow c - {1 \over 6}y\overrightarrow a - {1 \over 3}y\overrightarrow b \cr} \)
Do \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) không đồng phẳng nên điều đó tương đương với:
\(\eqalign{ & \left\{ \matrix{ - {2 \over 3}x - {1 \over 6}y = - {2 \over 3} \hfill \cr - {1 \over 3}y = - {1 \over 3} \hfill \cr {2 \over 3}x = k \hfill \cr} \right. \cr & \Rightarrow y = 1,x = {3 \over 4},k = {1 \over 2} \cr} \)
Vậy khi \(k = {1 \over 2}\) thì các điểm M, N, P, Q thuộc cùng một mặt phẳng.
