Bài 6. Cho hình vuông \(C_1\) có cạnh bằng \(4\). Người ta chia mỗi cạnh của hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông lại làm tiếp tục như trên để được hình vuông khác. Tiếp tục quá trình như trên, ta nhận được dãy các hình vuông. Gọi \(a_1\) là độ dài cạnh của hình vuông \(C_n\). Chứng minh dãy số \((a_n)\) là một cấp số nhân.
Hướng dẫn giải:
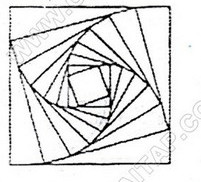
Xét dãy số \((a_n)\), ta có \(a_1= 4\).
Advertisements (Quảng cáo)
Giả sử hình vuông cạnh \(C_n\) có độ dài cạnh là \(a_n\). Ta sẽ tính cạnh \(a_{n+1}\) của hình vuông \(C_{n+1}\) Theo hình 44, áp dụng định lí Pi-ta-go, ta có:
\({a_{n + 1}} = \sqrt {{{\left( {{1 \over 4}{a_n}} \right)}^2} + {{\left( {{3 \over 4}{a_n}} \right)}^2}} = {a_n}.{{\sqrt {10} } \over 4}\forall n \in {\mathbb N}^*\)
Vậy dãy số \((a_n)\) là cấp số nhân với số hạng đầu là \(a_1= 4\) và công bội \(q = {{\sqrt {10} } \over 4}\).
