
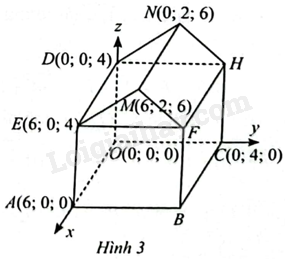
Một nhân viên đang sử dụng phần mềm để thiết kế khung của một ngôi nhà trong không gian \(Oxyz\) được minh hoạ như Hình 3. Cho biết \(OABC.DEFH\) là hình hộp chữ nhật và \(EMF.DNH\) là hình lăng trụ đứng.
a) Tìm toạ độ của các điểm \(B,F,H\).
b) Tìm toạ độ của các vectơ \(\overrightarrow {ME} ,\overrightarrow {MF} \).
c) Tính số đo \(\widehat {EMF}\).

‒ Sử dụng toạ độ của vectơ \(\overrightarrow {AB} = \left( {{x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A}} \right)\).
‒ Sử dụng tính chất hai vectơ bằng nhau: Với \(\overrightarrow u = \left( {{x_1};{y_1};{z_1}} \right)\) và \(\overrightarrow v = \left( {{x_2};{y_2};{z_2}} \right)\), ta có: \(\overrightarrow u = \overrightarrow v \Leftrightarrow \left\{ \begin{array}{l}{x_1} = {x_2}\\{y_1} = {y_2}\\{z_1} = {z_2}\end{array} \right.\).
‒ Sử dụng công thức tính góc của hai vectơ \(\overrightarrow u = \left( {{x_1};{y_1};{z_1}} \right)\) và \(\overrightarrow v = \left( {{x_2};{y_2};{z_2}} \right)\):
\(\cos \left( {\overrightarrow u ,\overrightarrow v } \right) = \frac{{\overrightarrow u .\overrightarrow v }}{{\left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|}} = \frac{{{x_1}.{x_2} + {y_1}.{y_2} + {z_1}.{z_2}}}{{\sqrt {x_1^2 + y_1^2 + z_1^2} .\sqrt {x_2^2 + y_2^2 + z_2^2} }}\).

a) Giả sử \(B\left( {{x_B};{y_B};{z_B}} \right)\). Ta có
\(\overrightarrow {OA} = \left( {6;0;0} \right),\overrightarrow {CB} = \left( {{x_B};{y_B} - 4;{z_B}} \right)\).
Advertisements (Quảng cáo)
\(OABC\) là hình chữ nhật nên \(\overrightarrow {OA} = \overrightarrow {CB} \).
\( \Leftrightarrow \left\{ \begin{array}{l}{x_B} = 6\\{y_B} - 4 = 0\\{z_B} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_B} = 6\\{y_B} = 4\\{z_B} = 0\end{array} \right.\). Vậy \(B\left( {6;4;0} \right)\).
Giả sử \(F\left( {{x_F};{y_F};{z_F}} \right)\). Ta có
\(\overrightarrow {A{\rm{E}}} = \left( {0;0;4} \right),\overrightarrow {BF} = \left( {{x_F} - 6;{y_F} - 4;{z_F}} \right)\).
\(ABF{\rm{E}}\) là hình chữ nhật nên \(\overrightarrow {A{\rm{E}}} = \overrightarrow {BF} \).
\( \Leftrightarrow \left\{ \begin{array}{l}{x_F} - 6 = 0\\{y_F} - 4 = 0\\{z_F} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_B} = 6\\{y_B} = 4\\{z_B} = 4\end{array} \right.\). Vậy \(F\left( {6;4;4} \right)\).
Giả sử \(H\left( {{x_H};{y_H};{z_H}} \right)\). Ta có
\(\overrightarrow {O{\rm{D}}} = \left( {0;0;4} \right),\overrightarrow {CH} = \left( {{x_H};{y_H} - 4;{z_H}} \right)\).
\(OCH{\rm{D}}\) là hình chữ nhật nên \(\overrightarrow {O{\rm{D}}} = \overrightarrow {CH} \).
\( \Leftrightarrow \left\{ \begin{array}{l}{x_H} = 0\\{y_H} - 4 = 0\\{z_H} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_H} = 0\\{y_H} = 4\\{z_H} = 4\end{array} \right.\). Vậy \(H\left( {0;4;4} \right)\).
b) \(\overrightarrow {ME} = \left( {6 - 6;0 - 2;4 - 6} \right) = \left( {0; - 2; - 2} \right),\overrightarrow {MF} = \left( {6 - 6;4 - 2;4 - 6} \right) = \left( {0;2; - 2} \right)\).
c) \(\cos \widehat {EMF} = \cos \left( {\overrightarrow {ME} ,\overrightarrow {MF} } \right) = \frac{{0.0 + \left( { - 2} \right).2 + \left( { - 2} \right).\left( { - 2} \right)}}{{\sqrt {{0^2} + {{\left( { - 2} \right)}^2} + {{\left( { - 2} \right)}^2}} .\sqrt {{0^2} + {2^2} + {{\left( { - 2} \right)}^2}} }} = 0\)
Vậy \(\widehat {EMF} = {90^ \circ }\).
