Bài 5 trang 17 SBT Toán 12 - Chân trời sáng tạo: Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau...

Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:

a) $y = \sqrt { - {x^2} + 9}$;

b) $y = \frac{{x + 1}}{{{x^2} + 2{\rm{x}} + 10}}$.

• Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số $f\left( x \right)$ trên đoạn $\left[ {a;b} \right]$:

Bước 1. Tìm các điểm ${x_1},{x_2},...,{x_n}$ thuộc khoảng $\left( {a;b} \right)$ mà tại đó $f’\left( x \right)$ bằng 0 hoặc không tồn tại.

Bước 2. Tính $f\left( a \right);f\left( {{x_1}} \right);f\left( {{x_2}} \right);...;f\left( {{x_n}} \right);f\left( b \right)$.

Bước 3. Gọi $M$ là số lớn nhất và $m$ là số nhỏ nhất trong các giá trị tìm được ở Bước 2. Khi đó: $M = \mathop {\max }\limits_{\left[ {a;b} \right]} f\left( x \right),m = \mathop {\min }\limits_{\left[ {a;b} \right]} f\left( x \right)$.

• Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng, đoạn hay nửa khoảng bằng đạo hàm:

‒ Lập bảng biến thiên của hàm số trên tập hợp đó.

‒ Căn cứ vào bảng biến thiên, kết luận giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số.

a) Tập xác định: $D = \left[ { - 3;3} \right]$.

Xét hàm số $y = f\left( x \right) = \sqrt { - {x^2} + 9}$ trên đoạn $\left[ { - 3;3} \right]$.

Ta có: $f’\left( x \right) = \frac{{{{\left( { - {x^2} + 9} \right)}^\prime }}}{{2\sqrt { - {x^2} + 9} }} = \frac{{ - 2{\rm{x}}}}{{2\sqrt { - {x^2} + 9} }} = \frac{{ - {\rm{x}}}}{{\sqrt { - {x^2} + 9} }}$

$f’\left( x \right) = 0 \Leftrightarrow x = 0$.

$f\left( { - 3} \right) = 0;f\left( 0 \right) = 3;f\left( 3 \right) = 0$

Vậy $\mathop {\max }\limits_{\left[ { - 3;3} \right]} f\left( x \right) = f\left( 0 \right) = 3,\mathop {\min }\limits_{\left[ { - 3;3} \right]} f\left( x \right) = f\left( 3 \right) = f\left( { - 3} \right) = 0$.

b) Tập xác định: $D = \mathbb{R}$.

Xét hàm số $y = f\left( x \right) = \frac{{x + 1}}{{{x^2} + 2{\rm{x}} + 10}}$ trên $\mathbb{R}$.

Ta có:

$\begin{array}{l}f’\left( x \right) = \frac{{{{\left( {x + 1} \right)}^\prime }\left( {{x^2} + 2{\rm{x}} + 10} \right) - \left( {x + 1} \right){{\left( {{x^2} + 2{\rm{x}} + 10} \right)}^\prime }}}{{{{\left( {{x^2} + 2{\rm{x}} + 10} \right)}^2}}}\\ & = \frac{{\left( {{x^2} + 2{\rm{x}} + 10} \right) - \left( {x + 1} \right)\left( {2{\rm{x}} + 2} \right)}}{{{{\left( {{x^2} + 2{\rm{x}} + 10} \right)}^2}}} = \frac{{ - {x^2} - 2{\rm{x}} + 8}}{{{{\left( {{x^2} + 2{\rm{x}} + 10} \right)}^2}}}\end{array}$

$f’\left( x \right) = 0 \Leftrightarrow x = 2$ hoặc ${\rm{x}} = - 4$.

Bảng biến thiên của hàm số:

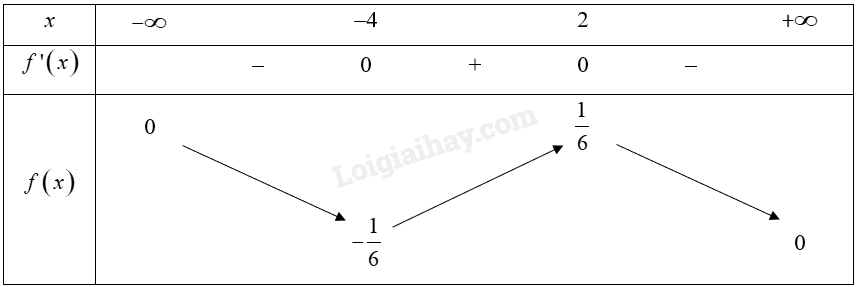
Từ bảng biến thiên, ta thấy $\max f\left( x \right) = f\left( 2 \right) = \frac{1}{6},\min f\left( x \right) = f\left( { - 4} \right) = - \frac{1}{6}$.