
Cho hình lập phương \(ABCD.A’B’C’D’\). Gọi \(O,O’\)lần lượt là tâm của các hình vuông \(ABCD\) và \(A’B’C’D’\); \(I\) là giao điểm của \(AC’\) và \(A’C\). Chứng minh rằng:
a) \(\overrightarrow {OA’} + \overrightarrow {OB’} + \overrightarrow {OC’} + \overrightarrow {OD’} = 4\overrightarrow {OO’} \);
b) \(\overrightarrow {DB} + \overrightarrow {DD’} = 2\overrightarrow {DI} \).

Sử dụng quy tắc hình bình hành.

Advertisements (Quảng cáo)
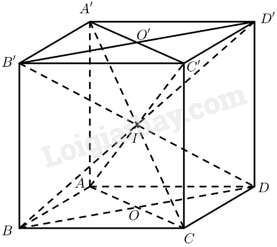
a) \(\overrightarrow {OA’} + \overrightarrow {OB’} + \overrightarrow {OC’} + \overrightarrow {OD’} = \left( {\overrightarrow {OA’} + \overrightarrow {OC’} } \right) + \left( {\overrightarrow {OB’} + \overrightarrow {OD’} } \right) = 2\overrightarrow {OO’} + 2\overrightarrow {OO’} = 4\overrightarrow {OO’} \)
b) Ta có: \(A’B’\parallel C{\rm{D}},A’B’ = C{\rm{D}}\)
Suy ra \(A’B’C{\rm{D}}\) là hình bình hành.
Do đó \(A’C\) và \(B’D\) cắt nhau tại trung điểm mỗi đường.
Vì \(I\) là trung điểm của \(A’C\) nên \(I\) là trung điểm của \(B’D\).
Suy ra \(\overrightarrow {DB} + \overrightarrow {DD’} = \overrightarrow {DB’} = 2\overrightarrow {DI} \).
