
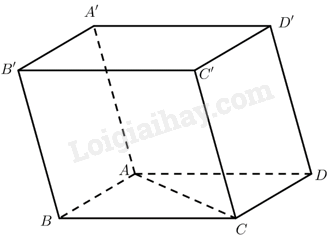
Cho hình hộp \(ABCD.A’B’C’D’\) có tất cả các cạnh bằng \(a\) và cho biết \(\widehat {BAD} = \widehat {BAA’} = \widehat {DAA’} = {60^ \circ }\). Tính các tích vô hướng sau:
a) \(\overrightarrow {AB} .\overrightarrow {AD} \);
b) \(\overrightarrow {DA} .\overrightarrow {DC} \);
c) \(\overrightarrow {AA’} .\overrightarrow {AC} \).

Sử dụng tích vô hướng của hai vectơ: \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\).
Advertisements (Quảng cáo)

a) \(\overrightarrow {AB} .\overrightarrow {AD} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AD} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AD} } \right) = AB.AD.\cos \widehat {BA{\rm{D}}} = a.a.\cos {60^ \circ } = \frac{{{a^2}}}{2}\).
b) \(\widehat {A{\rm{D}}C} = {180^ \circ } - \widehat {BAD} = {120^ \circ }\)
\(\overrightarrow {DA} .\overrightarrow {DC} = \left| {\overrightarrow {DA} } \right|.\left| {\overrightarrow {DC} } \right|.\cos \left( {\overrightarrow {DA} ,\overrightarrow {DC} } \right) = DA.DC.\cos \widehat {A{\rm{D}}C} = a.a.\cos {120^ \circ } = - \frac{{{a^2}}}{2}\).
c) \(\widehat {A{\rm{D}}C} = {180^ \circ } - \widehat {BAD} = {120^ \circ }\)
\(\begin{array}{l}\overrightarrow {AA’} .\overrightarrow {AC} = \overrightarrow {AA’} .\left( {\overrightarrow {AB} + \overrightarrow {AD} } \right) = \overrightarrow {AA’} .\overrightarrow {AB} + \overrightarrow {AA’} .\overrightarrow {AD} \\ = \left| {\overrightarrow {AA’} } \right|.\left| {\overrightarrow {AB} } \right|.\cos \left( {\overrightarrow {AA’} ,\overrightarrow {AB} } \right) + \left| {\overrightarrow {AA’} } \right|.\left| {\overrightarrow {AD} } \right|.\cos \left( {\overrightarrow {AA’} ,\overrightarrow {AD} } \right)\\ = AA’.AB.\cos \widehat {BAA’} + AA’.AD.\cos \widehat {DAA’} = a.a.\cos {60^ \circ } + a.a.\cos {60^ \circ } = \frac{{{a^2}}}{2} + \frac{{{a^2}}}{2} = {a^2}\end{array}\).
