
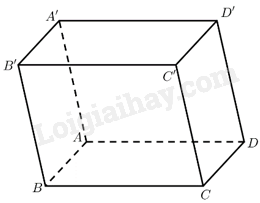
Cho hình hộp \(ABCD.A’B’C’D’\) có \(A\left( {2;0;2} \right),B\left( {4;2;4} \right),D\left( {2; - 2;2} \right),C’\left( {8;10; - 10} \right)\). Tìm toạ độ điểm \(A’\).

‒ Sử dụng toạ độ của vectơ \(\overrightarrow {AB} = \left( {{x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A}} \right)\).
‒ Sử dụng tính chất hai vectơ bằng nhau: Với \(\overrightarrow u = \left( {{x_1};{y_1};{z_1}} \right)\) và \(\overrightarrow v = \left( {{x_2};{y_2};{z_2}} \right)\), ta có: \(\overrightarrow u = \overrightarrow v \Leftrightarrow \left\{ \begin{array}{l}{x_1} = {x_2}\\{y_1} = {y_2}\\{z_1} = {z_2}\end{array} \right.\).

Giả sử \(D\left( {{x_C};{y_C};{z_C}} \right)\). Ta có
\(\overrightarrow {AD} = \left( {2 - 2; - 2 - 0;2 - 2} \right) = \left( {0; - 2;0} \right)\).
Advertisements (Quảng cáo)
\(\overrightarrow {BC} = \left( {{x_C} - 4;{y_C} - 2;{z_C} - 4} \right)\).
\(ABCD\) là hình bình hành nên \(\overrightarrow {AD} = \overrightarrow {BC} \).
\( \Leftrightarrow \left\{ \begin{array}{l}{x_C} - 4 = 0\\{y_C} - 2 = - 2\\{z_C} - 4 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_C} = 4\\{y_C} = 0\\{z_C} = 4\end{array} \right.\). Vậy \(C\left( {4;0;4} \right)\).
Giả sử \(A’\left( {{x_{A’}};{y_{A’}};{z_{A’}}} \right)\). Ta có
\(\overrightarrow {AA’} = \left( {{x_{A’}} - 2;{y_{A’}};{z_{A’}} - 2} \right)\).
\(\overrightarrow {CC’} = \left( {8 - 4;10 - 0; - 10 - 4} \right) = \left( {4;10; - 14} \right)\).
\(ABCD\) là hình bình hành nên \(\overrightarrow {AD} = \overrightarrow {BC} \).
\( \Leftrightarrow \left\{ \begin{array}{l}{x_{A’}} - 2 = 4\\{y_{A’}} = 10\\{z_{A’}} - 2 = - 14\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_{A’}} = 6\\{y_{A’}} = 10\\{z_{A’}} = - 12\end{array} \right.\). Vậy \(A’\left( {6;10; - 12} \right)\).
