
Cho tam giác \(ABC\) cân tại \(A\) nội tiếp trong đường tròn tâm \(O\), bán kính 1 cm. Đặt \(\widehat A = \alpha \left( {0
a) Viết biểu thức tính diện tích \(S\) của tam giác \(ABC\) theo \(\alpha \).
b) Tìm diện tích lớn nhất của tam giác \(ABC\).

Sử dụng công thức tính diện tích tam giác để tính diện tích \(S\left( \alpha \right)\), sau đó tìm giá trị lớn nhất của hàm số \(S\left( \alpha \right)\) trên khoảng \(\left( {0;\pi } \right)\).

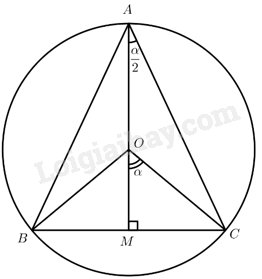
a) Gọi \(M\) là trung điểm của \(BC\), ta có:
\(\widehat {MOC} = 2\widehat {OAC} = \widehat {BAC} = \alpha \).
Do đó: \(AM = AO + OM = 1 + \cos \alpha ,BC = 2MC = 2\sin a\).
Advertisements (Quảng cáo)
Suy ra:
\(\begin{array}{l}S = \frac{1}{2}AM.BC = \frac{1}{2}2\sin \alpha \left( {1 + \cos \alpha } \right) = \sin \alpha \left( {1 + \cos \alpha } \right)\\ = \sin \alpha + \sin \alpha \cos \alpha = \sin \alpha + \frac{1}{2}\sin 2\alpha \end{array}\)
b) Xét hàm số \(S\left( \alpha \right) = \sin \alpha + \frac{1}{2}\sin 2\alpha \) trên khoảng \(\left( {0;\pi } \right)\).
Ta có: \(S’\left( \alpha \right) = \cos \alpha + \frac{1}{2}.2\cos 2\alpha = \cos \alpha + \cos 2\alpha = 2{\cos ^2}\alpha + \cos \alpha - 1\)
\(S’\left( \alpha \right) = 0 \Leftrightarrow \cos \alpha = \frac{1}{2}\) hoặc \(\cos \alpha = - 1\)
\(\alpha = \frac{\pi }{3}\) hoặc \(\alpha = \pi \) (loại)
Bảng biến thiên của hàm số trên khoảng \(\left( {0;\pi } \right)\):
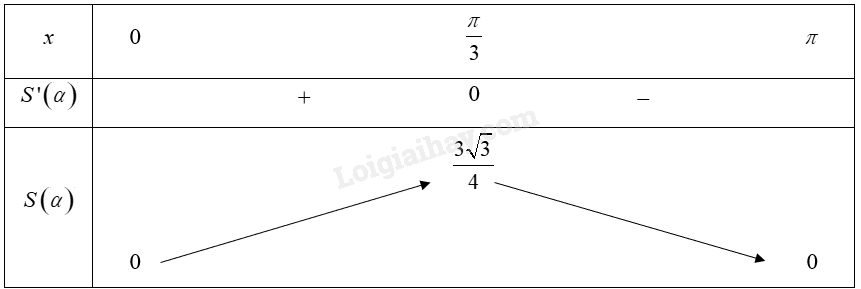
Từ bảng biến thiên, ta thấy \(\mathop {\max }\limits_{\left( {0;\pi } \right)} S\left( \alpha \right) = S\left( {\frac{\pi }{3}} \right) = \frac{{3\sqrt 3 }}{4}\).
Vậy tam giác \(ABC\) có diện tích lớn nhất bằng \(\frac{{3\sqrt 3 }}{4}\left( {c{m^2}} \right)\).
